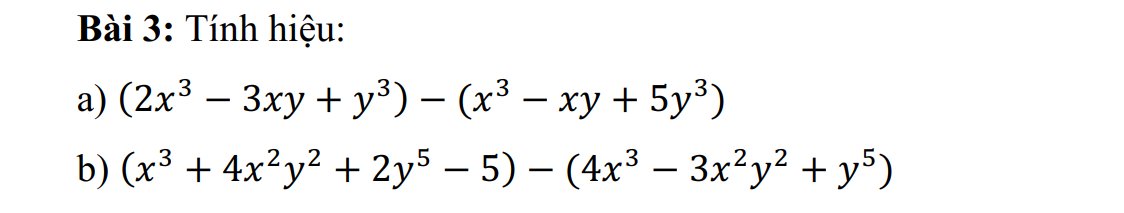\(a.\left(2x^3-3xy+y^3\right)-\left(x^3-xy+5y^3\right)\\ =2x^3-3xy+y^3-x^3+xy-5y^3\\ =\left(2x^3-x^3\right)+\left(-3xy+xy\right)+\left(y^3-5y^3\right)\\ =x^3-2xy-4y^3\\ b.\left(x^3+4x^2y^2+2y^5-5\right)-\left(4x^3-3x^2y^2+y^5\right)\\ =x^3+4x^2y^2+2y^5-5-4x^3+3x^2y^2-y^5\\ =\left(x^3-4x^3\right)+\left(4x^2y^2+3x^2y^2\right)+\left(2y^5-y^5\right)-5\\ =-3x^3+7x^2y^2+y^5-5\)
`(2x^3 - 3xy + y^3) - (x^3 - xy + 5y^3)`
`= 2x^3 - 3xy + y^3 - x^3 +xy - 5y^3`
`= (2x^3 - x^3) - (3xy - xy) + (y^3 -5y^3)`
`= x^3 - 2xy - 4y^3`
`(x^3 + 4x^2y^2 + 2y^5 - 5) - (4x^3 - 3x^2y^2 + y^5)`
`=x^3 + 4x^2y^2 + 2y^5 - 5 - 4x^3 + 3x^2y^2 - y^5`
`= (x^3 - 4x^3) + (4x^2y^2 + 3x^2y^2) + (2y^5 - y^5) - 5`
`= -3x^3 + 7x^2y^2 + y^5 - 5