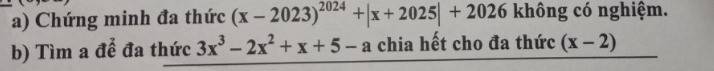a: (x-2023)^2024>=0
|x+2025|>=0
=>(x-2023)^2024+|x+2025|>=0
=>(x-2023)^2024+|x+2025|+2026>=2026>0 với mọi x
=>Đa thức này không có nghiệm
b: 3x^3-2x^2+x-a+5 chia hết cho x-2
=>3x^3-6x^2+4x^2-8x+9x-18-a+23 chia hết cho x-2
=>23-a=0
=>a=23
\(a)\) Ta thấy: \(\left(x-2023\right)^{2024}\ge0\forall x\)
\(\left|x+2025\right|\ge0\forall x\)
\(\Rightarrow\left(x-2023\right)^{2024}+\left|x+2025\right|\ge0\forall x\)
\(\Rightarrow\left(x-2023\right)^{2024}+\left|x+2025\right|+2026\ge2026>0\forall x\)
hay đa thức \(\left(x-2023\right)^{2024}+\left|x+2025\right|+2026\) không có nghiệm.
Vậy ...
\(b)\)Áp dụng định lý Bơ-du về số dư của phép chia đa thức vào phép chia hết của\(3x^3-2x^2+x+5-a\) cho \(x-2\), ta được:
Đa thức \(3x^3-2x^2+x+5-a\) có \(x=2\) là nghiệm
Khi đó: \(3\cdot2^3-2\cdot2^2+2+5-a=0\)
\(\Rightarrow24-8+7-a=0\)
\(\Rightarrow23-a=0\)
\(\Rightarrow a=23\)
Vậy ...
#Ayumu