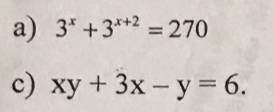a: =>3^x*10=270
=>3^x=27
=>x=3
c: =>x(y+3)-y-3=3
=>(x-1)(y+3)=3
=>\(\left(x-1;y+3\right)\in\left\{\left(1;3\right);\left(3;1\right);\left(-1;-3\right);\left(-3;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(2;0\right);\left(4;-2\right);\left(0;-6\right);\left(-2;-4\right)\right\}\)
`a,`
\(3^x+3^{x+2}=270\)
`->`\(3^x+3^x\cdot3^2=270\)
`->`\(3^x\left(1+3^2\right)=270\)
`->`\(3^x\cdot10=270\)
`->`\(3^x=270\div10\)
`->`\(3^x=27\)
`-> 3^x=3^3`
`-> x=3`
`c,` Tham khảo
\(xy+3x-y=6\)
`->`\(x\left(y+3\right)-y=6\)
`->`\(x\left(y+3\right)-y=3+3\)
`->`\(x\left(y+3\right)-y-3=3\)
`->`\(x\left(y+3\right)-\left(y+3\right)=3\)
`->`\(\left(x-1\right)\left(y+3\right)=3\)
`=>` \(\left(x-1\right)\text{và }\left(y+3\right)\inƯ\left(3\right)\)
Ta có bảng sau:
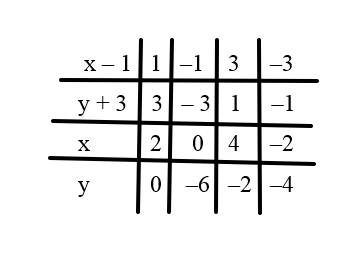
Vậy, tìm được `4` cặp \(\left\{x,y\right\}\): \(\left\{2;0\right\},\left\{0;-6\right\},\left\{4;-2\right\},\left\{-2;-4\right\}\)