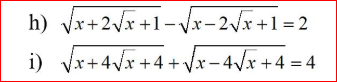i. ĐKXĐ: \(x\ge0\)
\(\sqrt{\left(\sqrt{x}+2\right)^2}+\sqrt{\left(\sqrt{x}-2\right)^2}=4\)
\(\Leftrightarrow\left|\sqrt{x}+2\right|+\left|\sqrt{x}-2\right|=4\)
\(\Leftrightarrow\left|\sqrt{x}+2\right|+\left|2-\sqrt{x}\right|=4\)
Mà theo BĐT trị tuyệt đối ta có:
\(\left|\sqrt{x}+2\right|+\left|2-\sqrt{x}\right|\ge\left|\sqrt{x}+2+2-\sqrt{x}\right|=4\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left(\sqrt{x}+2\right)\left(2-\sqrt{x}\right)\ge0\)
\(\Leftrightarrow2-\sqrt{x}\ge0\)
\(\Rightarrow x\le4\)
Kết hợp ĐKXD ta được nghiệm của pt là:
\(0\le x\le4\)
h.
ĐKXĐ: \(x\ge0\)
\(\sqrt{\left(\sqrt{x}+1\right)^2}-\sqrt{\left(\sqrt{x}-1\right)^2}=2\)
\(\Leftrightarrow\left|\sqrt{x}+1\right|-\left|\sqrt{x}-1\right|=2\)
\(\Leftrightarrow\sqrt{x}-\left|\sqrt{x}-1\right|=1\)
\(\Leftrightarrow\sqrt{x}-1=\left|\sqrt{x}-1\right|\)
\(\Leftrightarrow\sqrt{x}-1\ge0\) (sử dụng tính chất: \(A=\left|A\right|\Leftrightarrow A\ge0\))
\(\Leftrightarrow x\ge1\)
Vậy nghiệm của pt là \(x\ge1\)