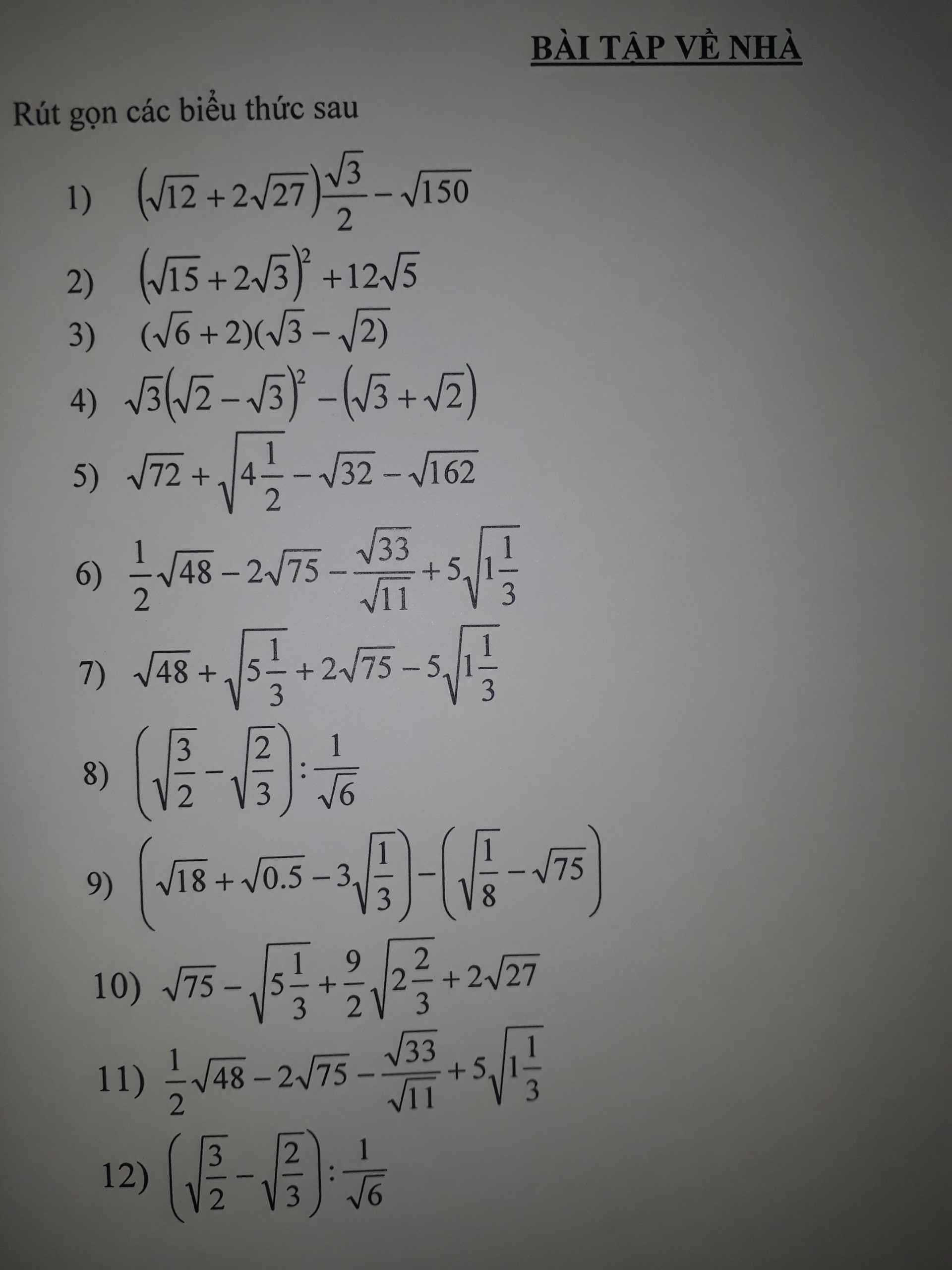1.
\(\left(\sqrt{12}+2\sqrt{27}\right)\dfrac{\sqrt{3}}{2}-\sqrt{150}\)
\(=\left(2\sqrt{3}+6\sqrt{3}\right)\dfrac{\sqrt{3}}{2}-5\sqrt{6}\)
\(=12-5\sqrt{6}\)
2.
\(\left(\sqrt{15}+2\sqrt{3}\right)^2+12\sqrt{5}\)
\(=27+12\sqrt{5}+12\sqrt{5}\)
\(=27+24\sqrt{5}\)
3.
\(\left(\sqrt{6}+2\right)\left(\sqrt{3}-\sqrt{2}\right)\)
\(=\sqrt{2}\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)\)
\(=\sqrt{2}\left(3-2\right)=\sqrt{2}\)
4.
\(\sqrt{3}\left(\sqrt{2}-\sqrt{3}\right)^2-\left(\sqrt{3}+\sqrt{2}\right)\)
\(=5\sqrt{3}-6\sqrt{2}-\sqrt{3}-\sqrt{2}\)
\(=4\sqrt{3}-7\sqrt{2}\)
8.
\(\left(\sqrt{\dfrac{3}{2}}-\sqrt{\dfrac{2}{3}}\right):\dfrac{1}{\sqrt{6}}\)
\(=\left(\dfrac{3}{\sqrt{2}.\sqrt{3}}-\dfrac{2}{\sqrt{2}.\sqrt{3}}\right).\sqrt{2}.\sqrt{3}\)
\(=1\)
11: Ta có: \(\dfrac{1}{2}\sqrt{48}-2\sqrt{75}-\dfrac{\sqrt{33}}{\sqrt{11}}+5\sqrt{1\dfrac{1}{3}}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{10}{3}\sqrt{3}\)
\(=-\dfrac{17\sqrt{3}}{3}\)
9.
\(\left(\sqrt{18}+\sqrt{0,5}-3\sqrt{\dfrac{1}{3}}\right)-\left(\sqrt{\dfrac{1}{8}}-\sqrt{75}\right)\)
\(=\left(3\sqrt{2}+\dfrac{\sqrt{2}}{2}-\sqrt{3}\right)-\left(\dfrac{\sqrt{2}}{4}-5\sqrt{3}\right)\)
\(=\dfrac{13\sqrt{2}}{4}+4\sqrt{3}\)