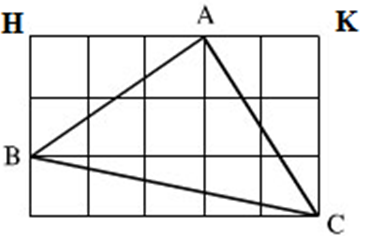
Tam giác ABC trên giấy kẻ ô vuông (h.151) là tam giác gì ? Vì sao ?
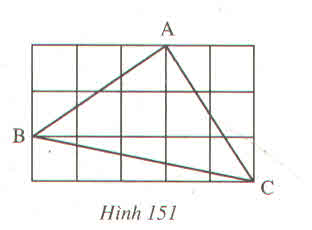
Tam giác ABC trên giấy kẻ ô vuông (h.151) là tam giác gì ? Vì sao ?

Đố vui :
Dũng đố Cường dùng 12 que diêm bằng nhau để xếp thành :
a) Một tam giác đều
b) Một tam giác cân mà không đều
c) Một tam giác vuông
Em hãy giúp Cường trong từng trường hợp trên ?
a) Xếp tam giác đều: Xếp tam giác với mỗi cạnh là bốn que diêm.
b) Một tam giác cân mà không đều: 2 cạnh bên 5 que diêm, cạnh đáy 2 que.
c) Xếp tam giác vuông: Xếp tam giác có các cạnh lần lượt là ba, bốn và năm que diêm. (Cạnh huyền 5 que diêm, 2 cạnh bên lần lượt là 3,4 que diêm).
Trả lời bởi Quang Duy
Đố :
Trên hình 152, một cầu trượt có đường lên BA dài 5m, độ cao AH là 3m, độ dài BC là 10m và CD là 2m. Bạn Mai nói rằng đường trượt tổng cộng ACD gấp hơn hai lần đường lên BA. Bạn Vân nói rằng điều đó không đúng. Ai đúng ? Ai sai ?

Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. Chứng minh rằng CD là đường trung trục của AB ?
Xét hai tam giác ACD và BCD có:
AC = BC (gt)
AD = BD (gt)
CD: cạnh chung
Vậy: \(\Delta ACD=\Delta BCD\left(c-c-c\right)\)
Suy ra: \(\widehat{C_1}=\widehat{C_2}\) (hai góc tương ứng)
Xét hai tam giác ACH và BCH có:
AC = BC (gt)
\(\widehat{C_1}=\widehat{C_2}\) (cmt)
CH: cạnh chung
Vậy: \(\Delta ACH=\Delta BCH\left(c-g-c\right)\)
Suy ra: \(\widehat{H_1}=\widehat{H_2}\), HA = HB
Mà \(\widehat{H_1}+\widehat{H_2}=180^o\)
Nên \(\widehat{H_1}=\widehat{H_2}\) = 90o
Do đó: \(CH\perp AB\)
Vì \(CD\perp AB\)và HA = HB nên CD là đường trung trực của AB.
Trả lời bởi Hải NgânCho tam ADE cân tại A. Trên cạnh DE lấy các điểm B và C sao cho \(DB=EC< \dfrac{1}{2}DE\)
a) Tam giác ABC là tam giác gì ? Chứng minh điều gì ?
b) Kẻ \(BM\perp AD,CN\perp AE\). Chứng minh rằng BM = CN
c) Gọi I là giao điểm của MB và NC. Tam giác IBC là tam giác gì ? Chứng minh điều đó
d) Chứng minh rằng AI là tia phân giác của góc BAC
a) Xét \(\Delta ABD\) và \(\Delta ACE\) ,có :
AD = AE ( Tam giác ADE cân tại A )
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
BD = CE ( gt )
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> AB = AC
=> \(\Delta ABC\) cân tại A
b) Xét \(\Delta BMD\) và \(\Delta CNE\) ,có :
BD = CE ( gt )
\(\widehat{BMD}=\widehat{CNE}=90^0\)
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A ) => \(\Delta BMD=\Delta CNE\left(ch-gn\right)\) => BM = CN c) Ta có : \(\widehat{MBD}=\widehat{NCE}\) ( \(\Delta BMD=\Delta CNE\) ) mà \(\widehat{MBD}=\widehat{IBC},\widehat{NCE}=\widehat{ICB}\) ( 2 góc đối đỉnh ) => \(\widehat{IBC}=\widehat{ICB}\) => Tam giác IBC cân tại I d) \(\Delta IAB=\Delta IAC\left(c.c.c\right)\) => \(\widehat{IAB}=\widehat{IAC}\) => AI là tia phân giác của góc BAC Trả lời bởi lê thị hương giangCho hình 69 trong đó \(AE\perp BC\)
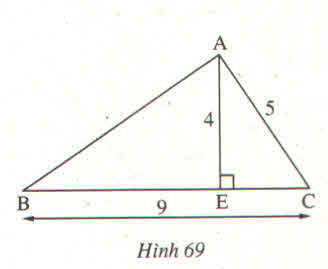
Tính AB biết AE = 4m, AC = 5m, BC = 9m
Tam giác AEC có góc AEC = \(90^0\)
=> \(AC^2=AE^2+EC^2\)
=>\(EC^2=AC^2-AE^2\)
=>\(EC^2=5^2-4^2\)
=>\(EC=\sqrt{9}=3\left(m\right)\)
Có EB + EC = BC
=>EB = BC - EC
=>EB = 9 - 3
=> EB = 6 (m)
Tam giác AEB có góc AEB = \(90^0\)
=>\(AB^2=AE^2+EB^2\)
=>\(AB^2=4^2+6^2\)
=>\(AB^2=16+36\)
=>\(AB^2=52\)
=>\(AB=\sqrt{52}=2\sqrt{13}\) (m)
Trả lời bởi Bùi Khánh ThiTìm các tam giác bằng nhau trên hình 70 ?
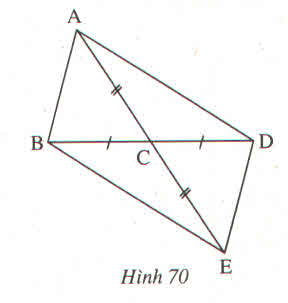
Các tam giác bằng nhau:
\(\Delta ABC=\Delta EDC\left(c-g-c\right)\)
\(\Delta ACD=\Delta ECB\left(c-g-c\right)\)
\(\Delta ABD=\Delta EDB\left(c-c-c\right)\)
\(\Delta ABE=\Delta EDA\left(c-c-c\right)\).
Trả lời bởi Hải Ngân
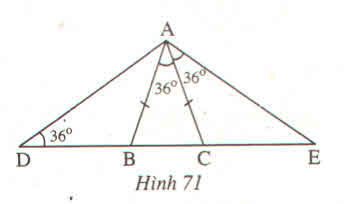
Tìm các tam giác cân trên hình 71 ?
Bạn Mai vẽ tia phân giác của một góc như sau : Đánh dấu trên hai cạnh của góc bốn đoạn thẳng bằng nhau : OA = AB = OC = CD
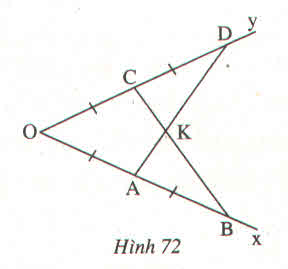
Kẻ các đoạn thẳng AD, BC, chúng cắt nhau ở K. Hãy giải thích vì sao OK là tia phân giác của góc O
Hướng dẫn : Chứng minh rằng :
a) \(\Delta OAD=\Delta OCB\)
b) \(\Delta KAB=\Delta KCD\)
Vì OA = AB = OC = CD
=> OD = OB
Xét \(\Delta OAD\)và \(\Delta OCB\)có:
OA = OC (gt)
\(\widehat{O}\)(chung)
OD = OB (cmt)
Do đó: \(\Delta OAD=\Delta OCB\) (c-g-c)
=> \(\widehat{ODA}=\widehat{OBC}\) (2 cạnh tương ứng)
=> \(\widehat{OCB}=\widehat{OAD}\) (2 cạnh tương ứng)
Vì \(\widehat{OCB}=\widehat{OAD}\) mà \(\widehat{OCB}+\widehat{DCB}=180^0\)(kề bù)
và \(\widehat{OAD}+\widehat{DAB}=180^0\)(kề bù)
Do đó: \(\widehat{DAB}=\widehat{BCD}\)
Xét \(\Delta KAB\)và \(\Delta KCD\)có:
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
AB = CD (gt)
\(\widehat{CDK}=\widehat{ABK}\left(\widehat{ODA}=\widehat{OBC}\right)\)
Do đó: \(\Delta KAB=\Delta KCD\left(g-c-g\right)\)
=> CK = KA (2 cạnh tương ứng)
Xét \(\Delta OCK\)và\(\Delta OAK\)có:
CK = KA(cmt)
OK (chung)
OA = OC (gt)
Do đó: \(\Delta OCK=\Delta OAK\left(c-c-c\right)\)
=> \(\widehat{COK}=\widehat{AOK}\) ( 2 góc tương ứng )
=> OK là tia phân giác \(\widehat{O}\)
Trả lời bởi Lê Vương Kim AnhCho tam giác ABC cân tại A, kẻ \(BH\perp AC\). Gọi D là một điểm thuộc cạnh đáy BC. Kẻ \(DE\perp AC,DF\perp AB\)
Chứng minh rằng \(DE+DF=BH\)
Kẻ DK \(\perp\) BH
Ta có: DK \(\perp\)BH
AC \(\perp\) BH
\(\Rightarrow\)DK // AC
\(\Rightarrow\) \(\widehat{BDK}=\widehat{C}\) (hai góc đồng vị) (1)
Vì \(\Delta ABC\) cân tại A \(\Rightarrow\) \(\widehat{DBF}=\widehat{C}\) (2)
Từ (1) và (2) suy ra: \(\widehat{BDK}=\widehat{DBF}\)
Xét hai tam giác vuông BDK và DBF có:
BD: cạnh huyền chung
\(\widehat{BDK}=\widehat{DBF}\) (cmt)
Vậy: \(\Delta BDK=\Delta DBF\left(ch-gn\right)\)
Suy ra: BK = DF (hai cạnh tương ứng) (3)
Ta lại có DE // KH, DK // EH nên chứng minh được: DE = KH (4)
Từ (3) và (4) suy ra: DE + DF = KH + BK = BH (đpcm).
Trả lời bởi Hải Ngân
Trả lời bởi Nguyễn Trần Thành Đạt