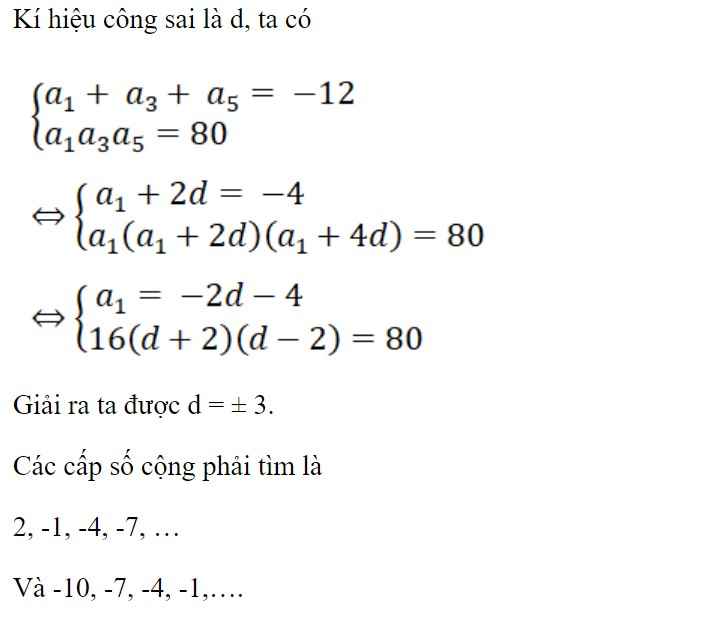Một tổ có 10 học sinh trong đó có An, Bình, Chi, Dung và Hương. Có bao nhiêu cách xếp 10 bạn đó vào 10 ghế sắp thành hàng ngang sao cho An, Bình ngồi cạnh nhau và Chi, Dung, Hương cũng ngồi cạnh nhau ?
Ôn tập cuối năm môn Đại số 11
SK
SK
Một trăm tấm thẻ như nhau được đánh số từ 1 đến 100. Lấy ngẫu nhiên một thẻ
Kí hiệu A và B là các biến cố :
A : " Thẻ được lấy ghi số chia hết cho 3"
B : "Thẻ được lấy ghi số chia hết cho 5"
a) Tính P(A), P(B) ?
b) A và B có độc lập không ? Vì sao ?
c) Cũng hỏi như trên nhưng số thẻ là 105 và được đánh số từ 1 đến 105 ?
SK
Có hai hộp chứa bi. Hộp thứ nhất chứa 1 bi đỏ và 2 bi xanh, hộp thứ hai chứa hai bi đỏ và 1 bi xanh. Từ mỗi hộp lấy ngẫu nhiên 1 bi. Tính xác xuất sao cho 2 bi lấy ra cùng mầu ?
SK
Tìm cấp số cộng \(a_1;a_2;a_3;a_4;a_5\) biết rằng :
\(a_1+a_3+a_5=-12\) và \(a_1a_3a_5=80\)
Hướng dẫn giải
Thảo luận (1)
SK
Viết 3 số hạng đầu của một cấp số cộng, biết rằng tổng n số hạng đầu tiên của cấp số này là :
\(S_n=4n^2-3n\)
Hướng dẫn giải
Thảo luận (1)
SK
Giải phương trình :
\(\dfrac{1}{x}+x+x^2+....+x^n+.....=\dfrac{7}{2}\)
trong đó \(\left|x\right|< 1\)
SK
Tìm số hạng thứ nhất \(a_1\) và công bội q của một cấp số nhân \(\left(a_n\right)\) biết rằng :
\(a_4-a_2=1\dfrac{13}{32}\) và \(a_6-a_4=-\dfrac{45}{512}\)
SK
Chứng minh rằng 3 số hạng đầu của tổng :
\(\dfrac{\sqrt{3}+1}{\sqrt{3}-1}+\dfrac{1}{3-\sqrt{3}}+\dfrac{1}{6}+.....\)
lập thành một cấp số nhân và tính tổng trên với giả thiết rằng các số hạng tiếp theo được tạo thành theo quy luật cấp số nhân đó
SK
Tính giới hạn \(\lim\limits_{n\rightarrow+\infty}x_n\) :
a) \(x_n=\dfrac{\sqrt{n}}{\sqrt{n+1}+\sqrt{n}}\)
b) \(x_n=\sqrt[3]{1+n^3}-n\)
c) \(x_n=n^2\left(n-\sqrt{n^2+1}\right)\)
d) \(x_n=\sqrt[3]{n^2-n^3}+n\)
SK
Tính giới hạn \(\lim\limits_{n\rightarrow+\infty}x_n\) :
a) \(x_n=\dfrac{\sqrt{n^2+1}+\sqrt{n}}{\sqrt[3]{n^3+n}-n}\)
b) \(x_n\left(n-\dfrac{1}{n}\right)\left(\dfrac{1-4n}{2n^2}\right)\)