Chứng minh rằng tam giác ABC vẽ trên giấy kẻ ô vuông là tam giác giác vuông cân (h.67) ?
Độ dài x trên hình bs 5 bằng :
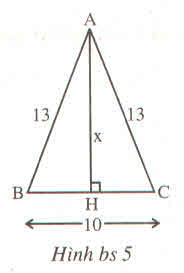
(A) \(\sqrt{69}\) (B) 10 (C) 11 (D) 12
Hãy chọn phương án đúng ?
Đáp án đúng là : (D) 12
Trả lời bởi Nguyễn Thị Thùy DươngMột tam giác vuông có các cạnh góc vuông tỉ lệ với 7 và 24, chu vi bằng 112 cm. Tính độ dài cạnh huyền ?
Gọi b, c là độ dài các cạnh góc vuông,a là độ dai cạnh huyền (tính bằng cm). Ta có:
\(\dfrac{b}{7}=\dfrac{c}{24}=k\Rightarrow b=7k,c=24k\)
Theo định lí Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
nên a = 25k
Theo đề bài a + b + c = 112 (cm). Từ đó ta tính được k = 2. Vậy a = 50cm.
Trả lời bởi Hải NgânTìm số tự nhiên a, biết rằng ba số 1, 8, 15 là độ dài ba cạnh của một tam giác vuông ?
Xét hai trường hợp :
- Trường hợp a là độ dài một cạnh góc vuông .
Từ a2 + 82 = 152 ,ta có a2 = 161 . Ta thấy 122 < a2 < 132 nên a không là số tự nhiên
- Trường hợp a là độ dài cạnh huyền
Từ a2 = 82 + 152 = 289 = 172 ,ta được a = 17
Vậy a = 17
Trả lời bởi Mai Hà Chi
Gọi độ dài cạnh của mỗi ô vuông là 1.
Theo định lí Py-ta-go:
AB2 = 12 + 22 = 1 + 4 = 5
BC2 = 12 + 22 = 1 + 4 = 5
AC2 = 12 + 32 = 1 + 9 = 10
Do AB2 = BC2 nên AB = BC
Do AB2 + BC2 = AC2 nên \(\widehat{ABC}=90^o\)
Vậy \(\Delta ABC\) vuông cân tại B.
Trả lời bởi Hải Ngân