Giải các phương trình :
a) \(\dfrac{1}{x}+2=\left(\dfrac{1}{x}+2\right)\left(x^2+1\right)\)
b) \(\left(x+1+\dfrac{1}{x}\right)^2=\left(x-1-\dfrac{1}{x}\right)^2\)
Giải các phương trình :
a) \(\dfrac{1}{x}+2=\left(\dfrac{1}{x}+2\right)\left(x^2+1\right)\)
b) \(\left(x+1+\dfrac{1}{x}\right)^2=\left(x-1-\dfrac{1}{x}\right)^2\)
Giải các phương trình :
a) \(\dfrac{1}{x-1}-\dfrac{3x^2}{x^3-1}=\dfrac{2x}{x^2+x+1}\)
b) \(\dfrac{3}{\left(x-1\right)\left(x-2\right)}+\dfrac{2}{\left(x-3\right)\left(x-1\right)}=\dfrac{1}{\left(x-2\right)\left(x-3\right)}\)
c) \(1+\dfrac{1}{x+2}=\dfrac{12}{8+x^3}\)
d) \(\dfrac{13}{\left(x-3\right)\left(2x+7\right)}+\dfrac{1}{2x+7}=\dfrac{6}{\left(x-3\right)\left(x+3\right)}\)
a)
Ta có:
cho nên x3 – 1 ≠ 0 khi x – 1 ≠ 0⇔ x ≠ 1
Vậy ĐKXĐ: x ≠ 1
Khử mẫu ta được:
Giải các phương trình :
a) \(\dfrac{1}{x-2}+3=\dfrac{x-3}{2-x}\)
b) \(2x-\dfrac{2x^2}{x+3}=\dfrac{4x}{x+3}+\dfrac{2}{7}\)
c) \(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}=\dfrac{4}{x^2-1}\)
d) \(\dfrac{3x-2}{x+7}=\dfrac{6x+1}{2x-3}\)
a) ĐKXĐ:
Khử mẫu ta được:
⇔
⇔4x = 8
⇔x = 2.
x = 2 không thỏa ĐKXĐ.
Vậy phương trình vô nghiệm.
b) ĐKXĐ:
Khử mẫu ta được:
=
Bạn Sơn giải phương trình :
\(\dfrac{x^2-5x}{x-5}=5\left(1\right)\)
\(\left(1\right)\Leftrightarrow x^2-5x=5\left(x-5\right)\)
\(\Leftrightarrow x^2-5x=5x-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x=5\)
Bạn Hà cho rằng Sơn giải sai vì đã nhân hai vế với biểu thức \(x-5\) có chứa ẩn. Hà giải bằng cách rút gọn vế trai như sau :
\(\left(1\right)\Leftrightarrow\dfrac{x\left(x-5\right)}{x-5}=5\Leftrightarrow x=5\)
Hãy cho biết ý kiến của em về hai lời giải trên ?
+ Trong cách giải của bạn Sơn có ghi
\(\left(1\right)x^2-5x=5\left(x-5\right)\)⇔ là sai vì x = 5 không là nghiệm của (1) hay (1) có ĐKXĐ: x ≠ 5.
+ Trong cách giải của Hà có ghi:
\(\left(1\right)\Leftrightarrow\dfrac{x\left(x-5\right)}{x-5}=5\Leftrightarrow x=5\)
Sai ở chỗ không tìm ĐKXĐ của phương trình mà lại rút gọn x – 5.
Tóm lại cả hai cách giải đều sai ở chỗ không tìm ĐKXĐ khi giải phương trình chứa ẩn ở mẫu.
Trả lời bởi qwertyGiải các phương trình :
a) \(\dfrac{2x-1}{x-1}+1=\dfrac{1}{x-1}\)
b) \(\dfrac{5x}{2x+2}+1=-\dfrac{6}{x+1}\)
c) \(x+\dfrac{1}{x}=x^2+\dfrac{1}{x^2}\)
d) \(\dfrac{x+3}{x+1}+\dfrac{x-2}{x}=2\)
a) ĐKXĐ: x # 1
Khử mẫu ta được: 2x - 1 + x - 1 = 1 ⇔ 3x = 3 ⇔ x = 1 không thoả mãn ĐKXĐ
Vậy phương trình vô nghiệm.
b) ĐKXĐ: x # -1
Khử mẫu ta được: 5x + 2x + 2 = -12
⇔ 7x = -14
⇔ x = -2
Vậy phương trình có nghiệm x = -2.
c) ĐKXĐ: x # 0.
Khử mẫu ta được: x3 + x = x4 + 1
⇔ x4 - x3 -x + 1 = 0
⇔ x3(x – 1) –(x – 1) = 0
⇔ (x3 -1)(x - 1) = 0
⇔ x3 -1 = 0 hoặc x - 1 = 0
1) x - 1 = 0 ⇔ x = 1
2) x3 -1 = 0 ⇔ (x - 1)(x2 + x + 1) = 0
⇔ x = 1 hoặc x2 + x + 1 = 0 ⇔ \(\left(x+\dfrac{1}{2}\right)^2=-\dfrac{3}{4}\) (vô lí)
Vậy phương trình có nghiệm duy nhất x = 1.
d) ĐKXĐ: x # 0 -1.
Khử mẫu ta được x(x + 3) + (x + 1)(x - 2) = 2x(x + 1)
⇔ x2 + 3x + x2 – 2x + x – 2 = 2x2 + 2x
⇔ 2x2 + 2x - 2 = 2x2 + 2x
⇔ 0x = 2
Phương trình 0x = 2 vô nghiệm.
Vậy phương trình đã cho vô nghiệm
Trả lời bởi qwertyGiải các phương trình
a) \(\dfrac{2x-5}{x+5}=3\)
b) \(\dfrac{x^2-6}{x}=x+\dfrac{3}{2}\)
c) \(\dfrac{\left(x^2+2x\right)-\left(3x+6\right)}{x-3}=0\)
d) \(\dfrac{5}{3x+2}=2x-1\)
a) ĐKXĐ: x # -5
\(\dfrac{2x-5}{x+5}=3\) ⇔ \(\dfrac{2x-5}{x+5}=\dfrac{3\left(x+5\right)}{x+5}\)
⇔ 2x - 5 = 3x + 15
⇔ 2x - 3x = 5 + 20
⇔ x = -20 thoả ĐKXĐ
Vậy tập hợp nghiệm S = {-20}
b) ĐKXĐ: x # 0
\(\dfrac{x^2-6}{x}=x+\dfrac{3}{2}\Leftrightarrow\dfrac{2\left(x^2+6\right)}{2x}=\dfrac{2x^2+3x}{2x}\)
Suy ra: 2x2 – 12 = 2x2 + 3x ⇔ 3x = -12 ⇔ x = -4 thoả x # 0
Vậy tập hợp nghiệm S = {-4}.
c) ĐKXĐ: x # 3
\(\dfrac{\left(x^2+2x\right)-\left(3x+6\right)}{x-3}=0\) ⇔ x(x + 2) - 3(x + 2) = 0
⇔ (x - 3)(x + 2) = 0 mà x # 3
⇔ x + 2 = 0
⇔ x = -2
Vậy tập hợp nghiệm S = {-2}
d) ĐKXĐ: x # \(-\dfrac{2}{3}\)
\(\dfrac{5}{3x+2}=2x-1\Leftrightarrow\dfrac{5}{3x+2}=\dfrac{\left(2x-1\right)\left(3x+2\right)}{3x+2}\)
⇔ 5 = (2x - 1)(3x + 2)
⇔ 6x2 – 3x + 4x – 2 – 5 = 0
⇔ 6x2 + x - 7 = 0
⇔ 6x2 - 6x + 7x - 7 = 0
⇔ 6x(x - 1) + 7(x - 1) = 0
⇔ (6x + 7)(x - 1) = 0
⇔ x = \(-\dfrac{7}{6}\) hoặc x = 1 thoả x # \(-\dfrac{2}{3}\)
Vậy tập nghiệm S = {1;\(-\dfrac{7}{6}\)}.
Trả lời bởi qwerty
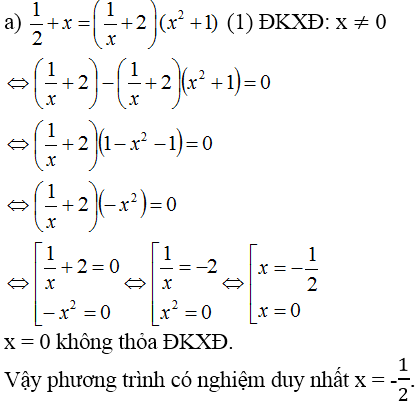

Trả lời bởi Phạm Thị Trâm Anh