Hình 6
Cho biết MN // BC, AB = 25 cm, BC = 45 cm, AM = 16 cm, AN = 10 cm
Tính độ dài x, y của các đoạn thẳng MN, AC ?
Hình 7
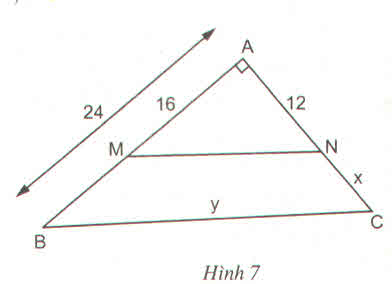
Cho biết tam giác ABC vuông tại A, MN // BC, AB = 24 cm, AM = 16 cm, AN = 12 cm. Tính độ dài x, y của các đoạn thẳng NC và BC ?
Hình thang ABCD (AB //CD) có hai đường chéo AC và BD cắt nhau tại O (h.8)
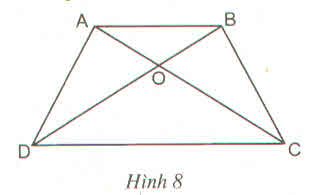
Chứng minh rằng :
\(OA.OD=OB.OC\)
Cho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q (h.9)
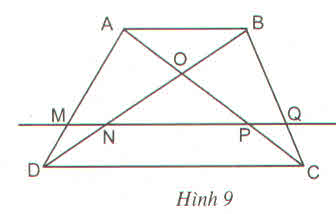
Chứng minh rằng MN = PQ ?
Cho hình thang ABCD (AB//CD). Trên cạnh bên AD lấy điểm E sao cho \(\dfrac{AE}{ED}=\dfrac{p}{q}\). Qua E kẻ đường thẳng song song với các đáy và cắt BC tại F (h.10)
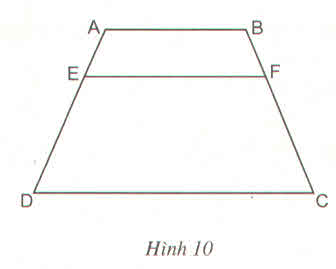
Chứng minh rằng :
\(EF=\dfrac{p.CD+q.AB}{p+q}\)
Hướng dẫn : Kẻ thêm đường chéo AC, cắt EF ở , rồi áp dụng hệ quả của định lí Ta - let vào các tam giác ADC và CAB
Hình thang cân ABCD (AB //CD) có hai đường chéo AC và BD cắt nhau tại O 9h.11).
Gọi M, N theo thứ tự là trung điểm của BD và AC. Cho biết MD = 3OM, đáy lớn CD = 5,6 cm
a) Tính độ dài đoạn thẳng MN và đáy nhỏ AB
b) So sánh độ dài đoạn thẳng MN với nửa hiệu các độ dài của CD và AB
Lời giải
a)
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)
Trả lời bởi ngonhuminhCho hình thang ABCD (AB //CD, AB < CD). Gọi trung điểm của các đường chéo AC, BD thứ tự là N và M (h.12).
Chứng minh rằng :
a) MN //AB
b) \(M=\dfrac{CD-AB}{2}\)
Lời giải
a)
Kẻ đường thẳng d qua M // với hai đáy
cắt AD tại P cắt BC tại Q cắt AC tại N'
Ta c/m N trùng N'
xét \(\Delta_{DBC}\) có MQ là đường trung bình tam giác => BQ=QC
PQ//DC => PQ là đường TB của Hình Thang ABCD => P là trung điểm của AD
xét \(\Delta_{DAC}\) có PQ là đường trung bình =>AN'=N'C
=> N' trùng N => MN //AB//CD=> dpcm
b)
???
Trả lời bởi ngonhuminhHình thang ABCD (AB //CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON (h.13)
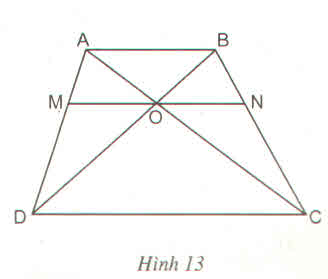
Xét tam giác ABC ta có:
ON // AB (gt)
=> \(\dfrac{ON}{AB}=\dfrac{CO}{CA}\left(1\right)\)\(\dfrac{ON}{AB}=\dfrac{CO}{CA}\left(2\right)\)
Xét tam giác ABD ta có:
OM // AB (gt)
=> \(\dfrac{OM}{AB}=\dfrac{DO}{DB}\left(2\right)\)
Vì AB // CD nên \(\dfrac{DO}{DB}=\dfrac{CO}{CA}\left(3\right)\)
Từ (1), (2) và (3) suy ra:
\(\dfrac{ON}{AB}=\dfrac{OM}{AB}=>OM=ON\)
Vậy OM = ON.
Trả lời bởi Dương NguyễnCho trước 3 đoạn thẳng có độ dài tương ứng là m, n và p. Dựng đoạn thẳng thứ tư có độ dàu q sao cho \(\dfrac{m}{n}=\dfrac{p}{q}\) ?
Cho ba đoạn thẳng AB = 3cm, CD = 5cm, EF = 2cm. Dựng đoạn thẳng thứ tư có độ dài a sao cho \(\dfrac{AB}{CD}=\dfrac{EF}{a}\) hay \(\dfrac{3}{5}=\dfrac{2}{a}\)
Tính giá trị của a ?
Trả lời bởi Nguyen Thuy Hoa