Cho tam giác \(ABC\) có \(AB=12cm\), \(AC=18cm\), \(AC=27cm\). Một điểm \(D\) thuộc cạnh \(BC\) sao cho \(CD=12cm\). Tính độ dài \(AD\)?
12cm.6cm.10cm.8cm.Hướng dẫn giải: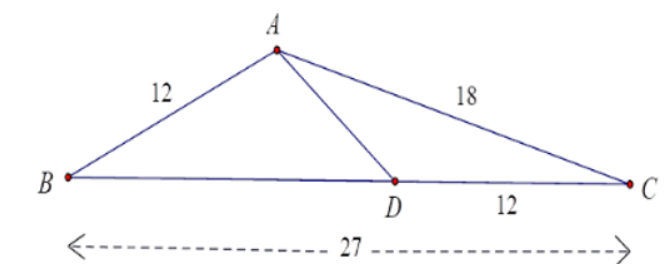
Có: \(\dfrac{AC}{DC}=\dfrac{18}{12}=\dfrac{3}{2}\) ; \(\dfrac{BC}{AC}=\dfrac{27}{18}=\dfrac{3}{2}\) \(\Rightarrow\) \(\dfrac{AC}{DC}=\dfrac{BC}{AC}=\dfrac{3}{2}\)
Xét \(\Delta CAB\) và \(\Delta CDA\) có:
\(\dfrac{AC}{DC}=\dfrac{BC}{AC}=\dfrac{3}{2}\)
\(\widehat{C}\) chung
\(\Rightarrow\) \(\Delta CAB\) đồng dạng với \(\Delta CDA\) (c.g.c) theo tỉ số \(\dfrac{3}{2}\)
\(\Rightarrow\) \(\dfrac{AB}{AD}=\dfrac{3}{2}\Rightarrow AD=8\)
