Cho tam giác \(ABC\) có \(AB< AC\). Điểm \(D\) thuộc \(AC\) sao cho \(AD=AB\). Gọi \(E\) là điểm nằm trong tam giác \(ABC\) sao cho \(EB=ED\). Khi đó:
\(\Delta ABE=\Delta ADE\).\(\Delta AEB=\Delta ADE\).\(\Delta ABE=\Delta DAE\).\(\widehat{AED}=\widehat{ABE}\).Hướng dẫn giải: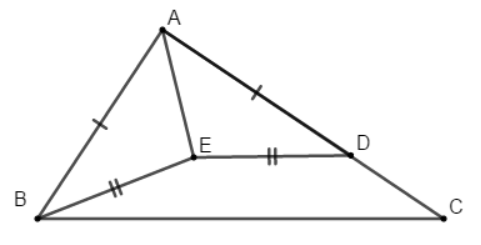
Xét \(\Delta ABE\) và \(\Delta ADE\) có:
\(AB=AD\) (gt)
\(AE\) chung
\(EB=ED\) (gt)
\(\Rightarrow\) \(\Delta ABE=\Delta ADE\) (c.c.c)
\(\Rightarrow\)A đúng , B,C,D sai.
