Cho hình bình hành \(ABCD\). Trên đường chéo \(AC\) lấy điểm \(E\) sao cho \(AC=3AE\). Qua \(E\) kẻ đường thẳng song song với \(CD\) cắt \(AD,BC\) tại \(M,N\). Cho các khẳng định sau:
(I) \(\Delta AME\) đồng dạng với \(\Delta ADC\) theo tỉ số \(k_1=\dfrac{1}{3}\).
(II) \(\Delta CBA\) đồng dạng với \(\Delta ADC\) theo tỉ số \(k_2=1\).
(III) \(\Delta CNE\) đồng dạng với \(\Delta ADC\) theo tỉ số \(k_3=\dfrac{2}{3}\).
Chọn câu đúng.
(I) đúng, (II) và (III) sai.(I) và (II) đúng, (III) sai.Cả (I), (II), (III) đúng.Cả (I), (II), (III) sai.Hướng dẫn giải: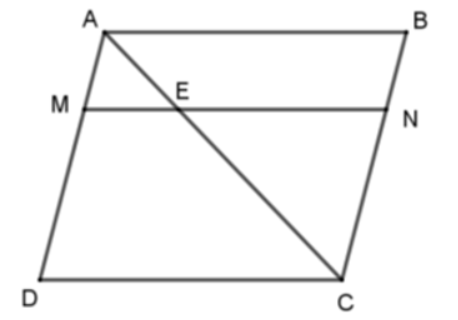
Do \(ABCD\) là hình bình hành \(\Rightarrow\) ME//DC, EN//AB
+) Do ME//DC nên \(\Delta AME\) đồng dạng với \(\Delta ADC\) theo tỉ số \(k_1=\dfrac{AE}{AC}=\dfrac{1}{3}\) nên (I) đúng.
+) Có: \(AD=BC\), \(DC=AB\), \(AC\) chung suy ra \(\Delta CBA\) đồng dạng với \(\Delta ADC\) theo tỉ số \(k_2=\dfrac{AD}{BC}=1\) nên (II) đúng.
+) Do EN//AB nên \(\Delta CNE\) đồng dạng với \(\Delta CBA\) theo tỉ số \(\dfrac{CE}{AC}=\dfrac{2}{3}\) mà \(\Delta CBA\) đồng dạng với \(\Delta ADC\) theo tỉ số \(k_2=1\)
nên \(\Delta CNE\) đồng dạng với \(\Delta ADC\) theo tỉ số \(k_3=\dfrac{2}{3}.1=\dfrac{2}{3}\) nên (III) đúng.
