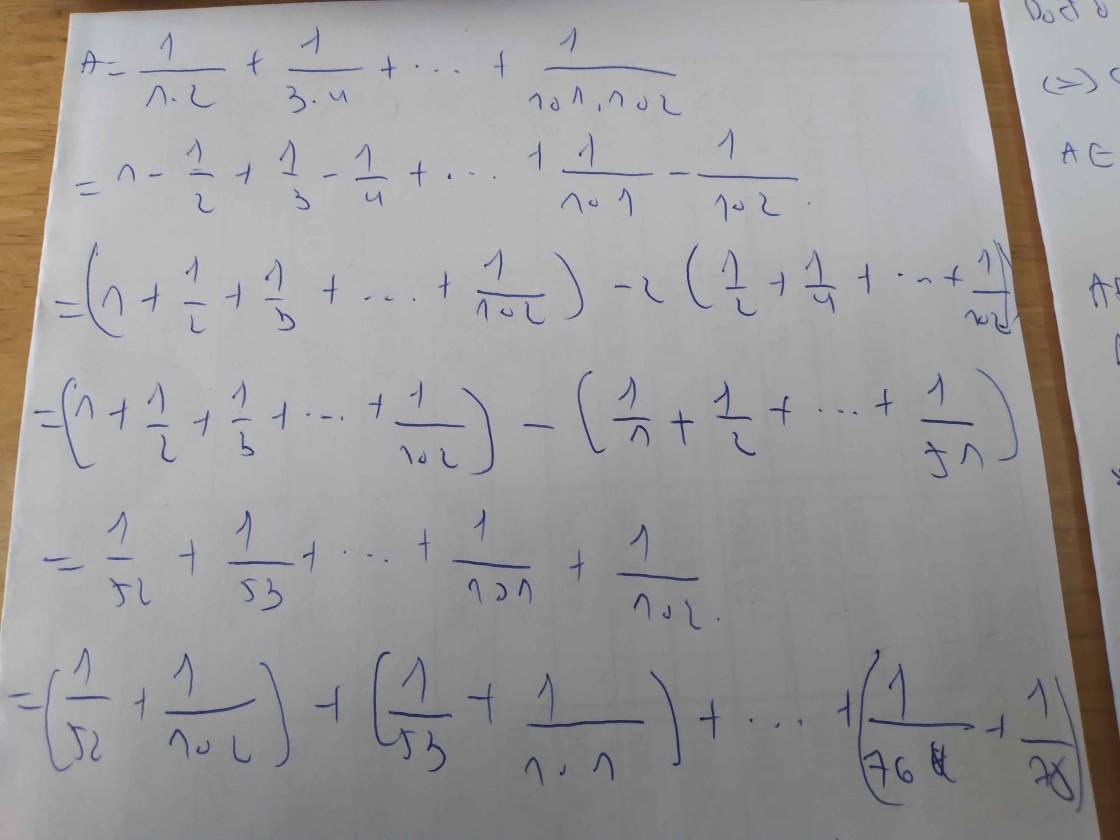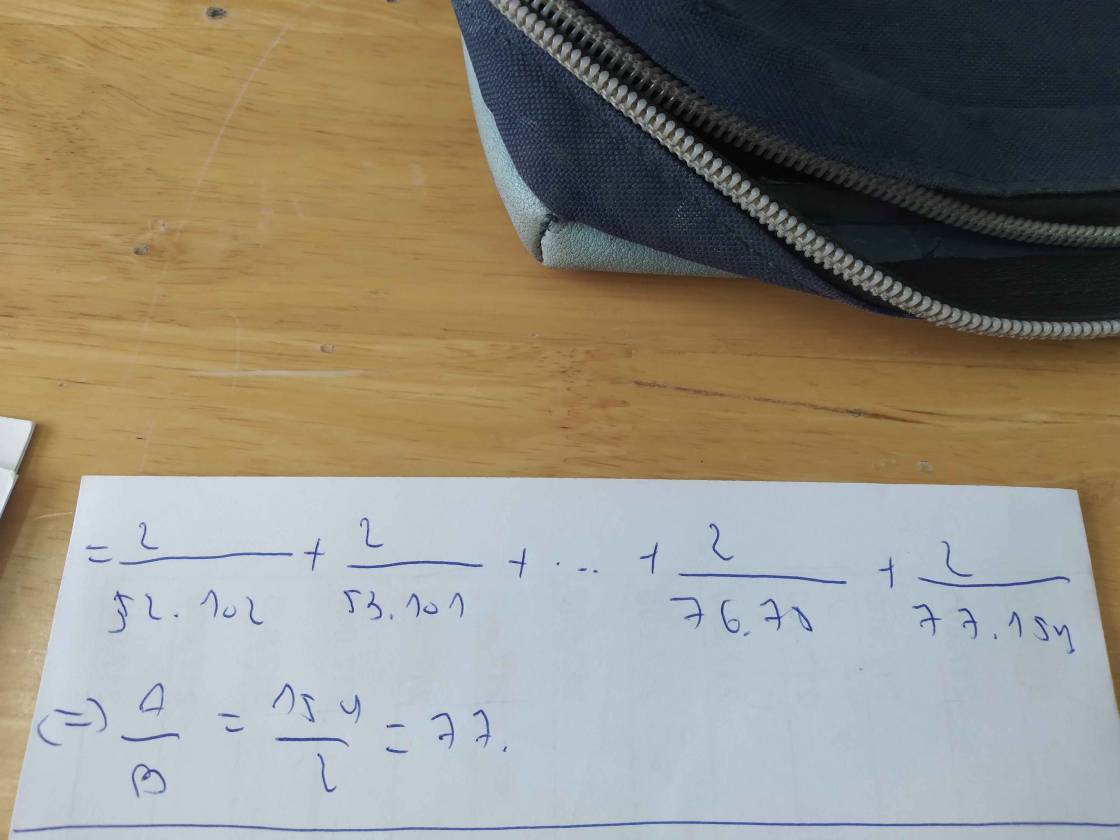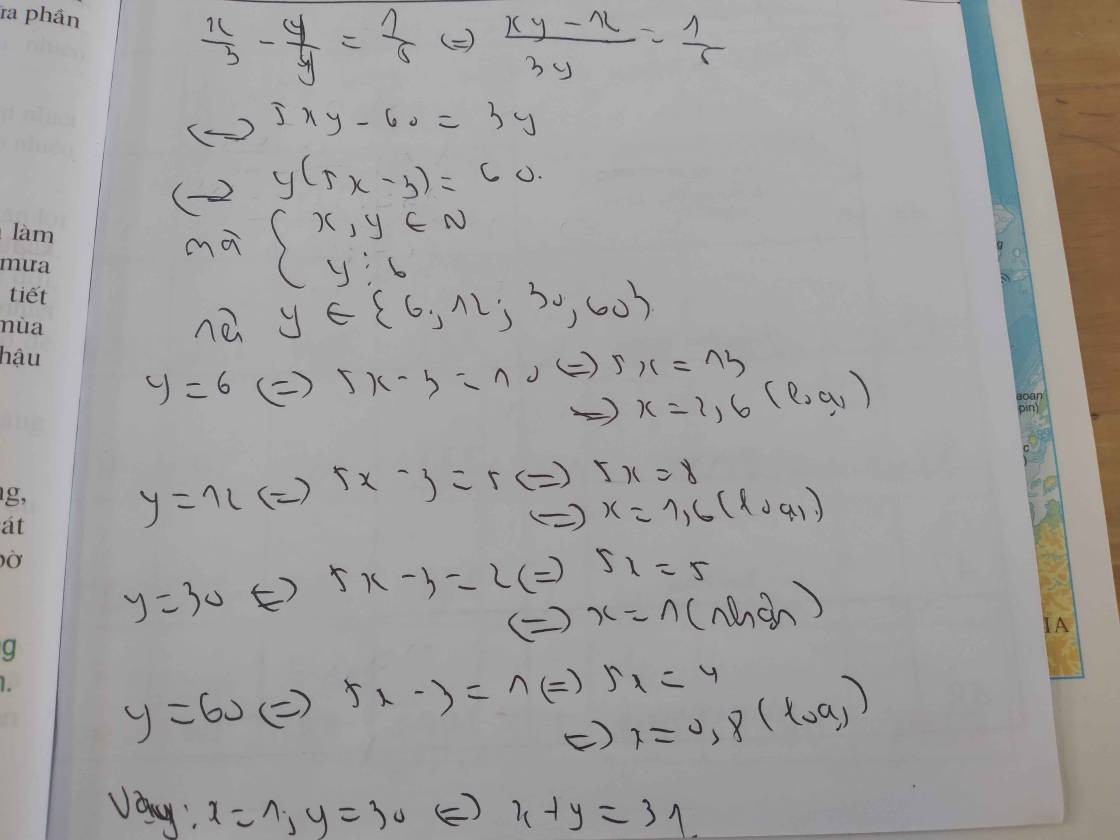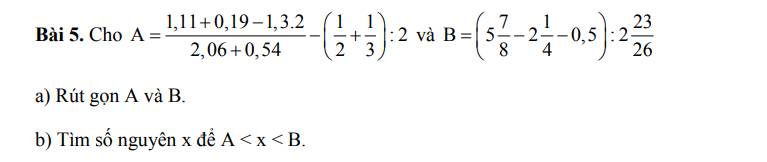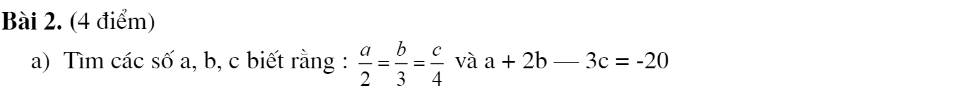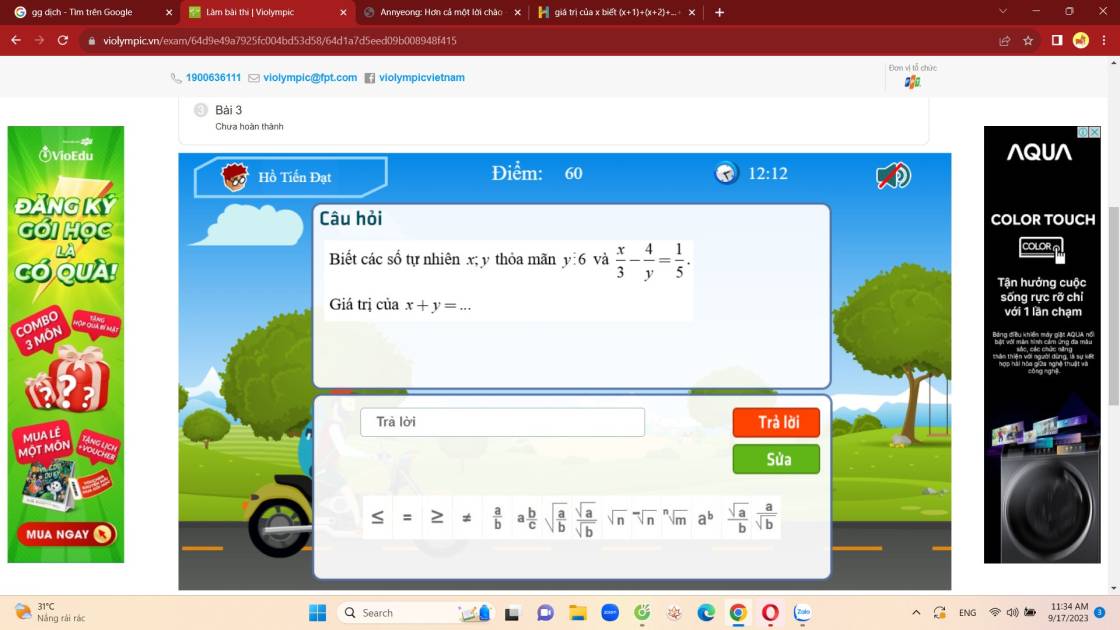
Violympic toán 7

\(\dfrac{1}{7}+\dfrac{1}{91}+...+\dfrac{1}{1147}\)

\(=\dfrac{1}{1\cdot7}+\dfrac{1}{7\cdot13}+\dfrac{1}{13\cdot19}+...+\dfrac{1}{31\cdot37}\)

\(=\dfrac{1}{6}\cdot\left(\dfrac{6}{1\cdot7}+\dfrac{6}{7\cdot13}+\dfrac{6}{13\cdot19}+...+\dfrac{6}{31\cdot37}\right)\)

\(=\dfrac{1}{6}\cdot\left(1-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{19}+...+\dfrac{1}{31}-\dfrac{1}{37}\right)\)

\(=\dfrac{1}{6}\cdot\left(1-\dfrac{1}{37}\right)\)

\(=\dfrac{1}{6}\cdot\dfrac{36}{37}\)

\(=\dfrac{6}{37}\)

Vậy ...

#\(Toru\)

\(S=\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{9999}\)

\(=\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{99\cdot101}\)

\(=\dfrac{1}{2}\cdot\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{99\cdot101}\right)\)

\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\)

\(=\dfrac{1}{2}\cdot\left(\dfrac{1}{3}-\dfrac{1}{101}\right)\)

\(=\dfrac{1}{2}\cdot\dfrac{98}{303}\)

\(=\dfrac{49}{303}\)

Vậy \(S=\dfrac{49}{303}\)

#\(Toru\)

\(< =>\dfrac{30x^2}{60}+\dfrac{20y^2}{60}+\dfrac{15z^2}{60}=\dfrac{12x^2+12y^2+12z^2}{60}\\ < =>30x^2+20y^2+15z^2=12x^2+12y^2+12z^2\\ < =>18x^2+8y^2+3z^2=0\)

có \(\left\{{}\begin{matrix}x^2\ge0\\y^2\ge0\\z^2\ge0\end{matrix}\right.< =>\left\{{}\begin{matrix}18x^2\ge0\\8y^2\ge0\\3z^2\ge0\end{matrix}\right.\)

`=>18x^2+8y^2+3z^2>=0`

dấu ''='' xảy khi \(\left\{{}\begin{matrix}18x^2=0\\8y^2=0\\3z^2=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=0\\y=0\\z=0\end{matrix}\right.\)

á bài khó qué 🫤

\(\dfrac{x^2}{2}+\dfrac{y^2}{3}+\dfrac{z^2}{4}=\dfrac{x^2+y^2+z^2}{5}\\ \Rightarrow\dfrac{30x^2+20y^2+15z^2}{60}=\dfrac{12x^2+12y^2+12z^2}{60}\\ \Rightarrow18x^2+8y^2+3z^2=0\)

Do \(x^2\ge0\forall x;y^2\ge0\forall y;z^2\ge0\forall z\)

\(\Rightarrow18x^2+8y^2+3z^2\ge0\)

Dấu "=" xảy ra khi \(x=y=z=0\)

\(\dfrac{x^2}{2}\)+\(\dfrac{y^2}{3}\) +\(\dfrac{z^2}{4}\) =\(\dfrac{x^2+y^2+z^2}{5}\) 

⇒\(30x^2\)+\(20y^2\)+\(15z^2\)=\(12x^2\)+\(12y^2\)+\(12z^2\) 

⇒\(18x^2\)+\(8y^2\)+ \(3z^2\)=0

⇒\(18x^2\)≥0 \(8y^2\)≥0 \(3z^2\)≥0

Nên \(18x^2\) + \(8y^2\) + \(3z^2\) ≥0

Vậy \(18x^2\) + \(8y^2\) + \(3z^2\)= 0

Khi và chỉ khi:

\(18x^2\)= 0;\(8y^2\)= 0;\(3z^2\)= 0

Vậy x=y=z=0

a: \(A=\dfrac{1.3-2.6}{2.6}-\dfrac{5}{6}:2=\dfrac{-1}{2}-\dfrac{5}{12}=-\dfrac{11}{12}\)

\(B=\left(5+\dfrac{7}{8}-2-\dfrac{1}{4}-\dfrac{1}{2}\right):\dfrac{75}{26}=\left(3+\dfrac{1}{8}\right):\dfrac{75}{26}\)

\(=\dfrac{25}{8}\cdot\dfrac{26}{75}=\dfrac{1}{3}\cdot\dfrac{13}{4}=\dfrac{13}{12}\)

b: A<x<B

=>-11/12<x<13/12

=>\(x\in\left\{0;1\right\}\)

a) \(A=\dfrac{1,11+0,19-1,3\cdot2}{2,06+0,54}-\left(\dfrac{1}{2}+\dfrac{1}{3}\right):2\)

\(A=\dfrac{\left(1,11+0,19\right)-2,6}{2,6}-\left(\dfrac{3}{6}+\dfrac{2}{6}\right):2\)

\(A=\dfrac{1,3-2,6}{2,6}-\dfrac{5}{6}:2\)

\(A=\dfrac{-1,3}{2,6}-\dfrac{5}{6}:2\)

\(A=\dfrac{-1}{2}-\dfrac{5}{12}\)

\(A=\dfrac{-6}{12}-\dfrac{5}{12}\)

\(A=-\dfrac{11}{12}\)

\(B=\left(5\dfrac{7}{8}-2\dfrac{1}{4}-0,5\right):2\dfrac{23}{26}\)

\(B=\left(5+\dfrac{7}{8}-2-\dfrac{1}{4}-\dfrac{1}{2}\right):\dfrac{23+26+26}{26}\)

\(B=\left(3+\dfrac{7}{8}-\dfrac{2}{8}-\dfrac{4}{8}\right):\dfrac{75}{26}\)

\(B=\left(3+\dfrac{1}{8}\right)\cdot\dfrac{26}{75}\)

\(B=\left(\dfrac{24}{8}+\dfrac{1}{8}\right)\cdot\dfrac{26}{75}\)

\(B=\dfrac{25}{8}\cdot\dfrac{26}{75}\)

\(B=\dfrac{26}{24}\)

\(B=\dfrac{13}{12}\)

b) Ta có:

\(A< x< B\)

\(\Rightarrow-\dfrac{11}{12}< x< \dfrac{13}{12}\)

\(\Rightarrow x\in\left\{0;1\right\}\)

\(C=\left(2+5+8+\cdot\cdot\cdot+98\right)\cdot\dfrac{1^2+2^2+3^2+4^2-2\cdot3\cdot5}{1-3+5-7+\cdot\cdot\cdot+97-99}\)

\(=\left(2+5+8+\cdot\cdot\cdot+98\right)\cdot\dfrac{1+4+9+16-30}{1-3+5-7+\cdot\cdot\cdot+97-99}\)

\(=\left(2+5+8+\cdot\cdot\cdot+98\right)\cdot\dfrac{0}{1-3+5-7+\cdot\cdot\cdot+97-99}\)

\(=0\)

#\(Toru\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+2b-3c}{2+2\cdot3-3\cdot4}=\dfrac{-20}{8-12}=5\)

=>a=10; b=15; c=20

Lời giải:
$(x-6^2)^2-\frac{1}{25}=0$

$\Rightarrow (x-36)^2=\frac{1}{25}=(\frac{1}{5})^2=(\frac{-1}{5})^2$

$\Rightarrow x-36=\frac{1}{5}$ hoặc $x-36=\frac{-1}{5}$

$\Rightarrow x=36\frac{1}{5}$ hoặc $x=35\frac{4}{5}$

Vậy có 2 giá trị $x$ thỏa mãn.