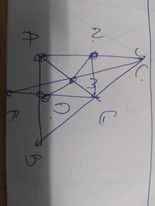
a: Xét ΔABC có
E là trung điểm của BC
D là trung điểm của BA
Do đó: ED là đường trung bình của ΔABC
=>ED//AC và \(ED=\dfrac{AC}{2}\)
Ta có: ED//AC
F\(\in\)ED
Do đó: EF//AC
Ta có: ED//AC
AB\(\perp\)AC
Do đó: ED\(\perp\)AB
=>EF\(\perp\)AB
Ta có: \(ED=\dfrac{AC}{2}\)
\(ED=\dfrac{EF}{2}\)
Do đó: AC=EF
Xét tứ giác AEBF có
D là trung điểm chung của AB và EF
=>AEBF là hình bình hành
Hình bình hành AEBF có AB\(\perp\)EF
nên AEBF là hình thoi
b: Xét tứ giác ECAF có
FE//AC
FE=AC
Do đó: ECAF là hình bình hành
c: ta có: ECAF là hình bình hành
=>EA cắt FC tại trung điểm của mỗi đường
mà M là trung điểm của EA
nên M là trung điểm của FC
=>C,M,F thẳng hàng
d: Ta có: \(DF=\dfrac{EF}{2}\)
\(CN=\dfrac{CA}{2}\)
mà EF=CA
nên DF=CN
Xét tứ giác DFNC có
DF//NC
DF=NC
Do đó: DFNC là hình bình hành
=>DN cắt FC tại trung điểm của mỗi đường
mà M là trung điểm của CF
nên M là trung điểm của DN
Xét tứ giác ADEN có
M là trung điểm chung của AE và DN
=>ADEN là hình bình hành
Hình bình hành ADEN có \(\widehat{DAN}=90^0\)
nên ADEN là hình chữ nhật
e: Khi BEAF là hình vuông thì \(\widehat{AEB}=90^0\)
=>AE\(\perp\)EB tại E
=>AE\(\perp\)BC tại E
Xét ΔABC có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔABC cân tại A
Xét ΔABC cân tại A có \(\widehat{BAC}=90^0\)
nên ΔABC vuông cân tại A
=>Điều này đúng
Ta có: ΔABC cân tại A
mà AE là đường trung tuyến
nên AE là phân giác của góc BAC
Hình chữ nhật ADEN có AE là phân giác của góc DAN
nên ADEN là hình vuông


