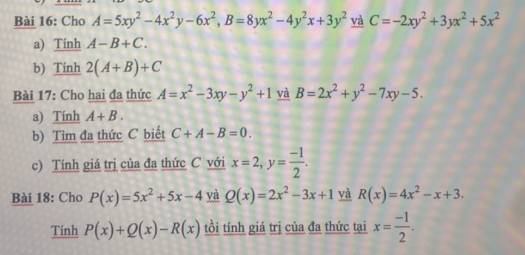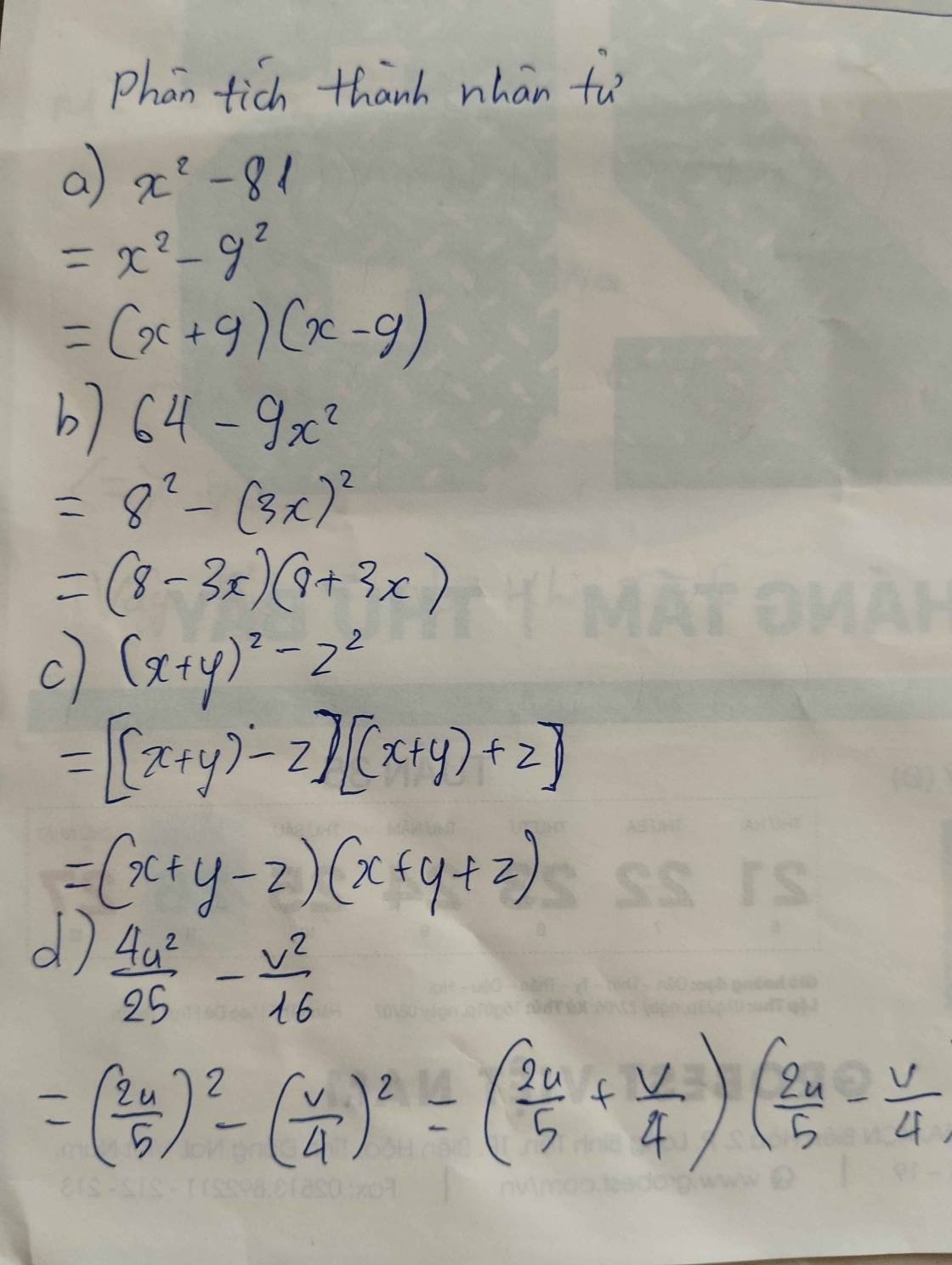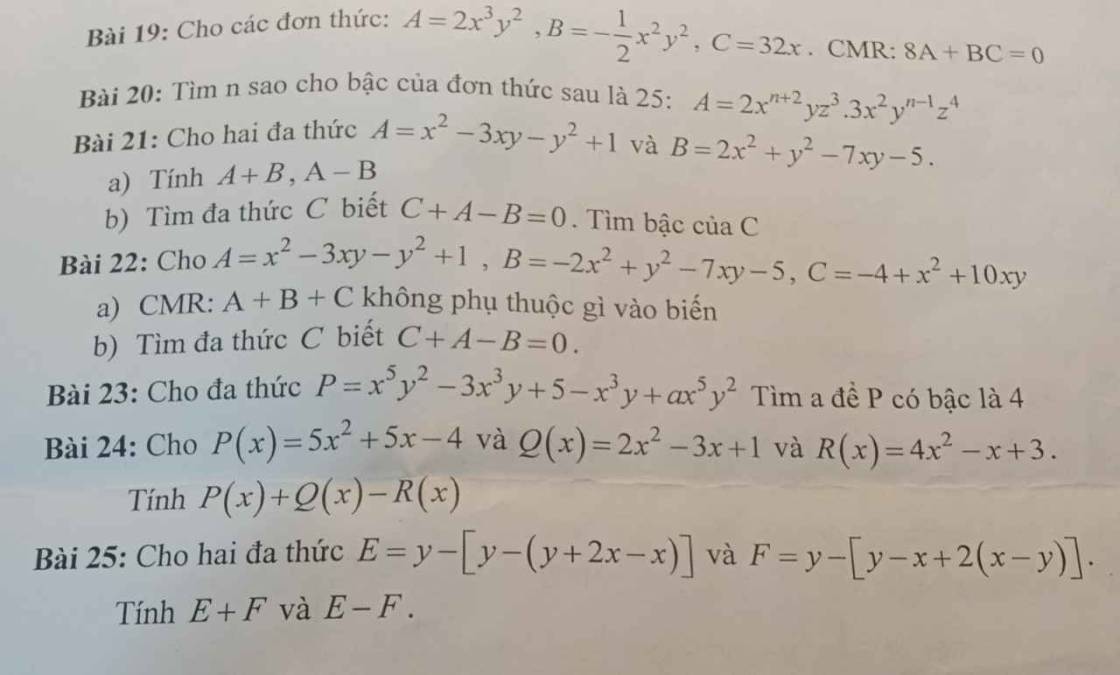Phép nhân và phép chia các đa thức
Bài 3:
1) \(\left(3x^2-4\right)\left(x+3y\right)\)
\(=3x^3+9x^2y-4x-12y\)
2) \(\left(x+3\right)\left(x^2+3x\right)\)
\(=x^3+3x^2+3x^2+9x\)
\(=x^3+6x^2+9x\)
3) \(\left(xy-1\right)\left(xy+5\right)\)
\(=x^2y^2+5xy-xy-5\)
\(=x^2y^2+4xy-5\)
4) \(\left(3x+5y\right)\left(2x-7y\right)\)
\(=6x^2-21xy+10xy-35y^2\)
\(=6x^2-11xy-35y^2\)
5) \(-\left(x-1\right)\left(-x^2+2y\right)\)
\(=\left(x-1\right)\left(x^2-2y\right)\)
\(=x^3-2xy-x^2+2y\)
6) \(\left(-x^2+2y\right)\left(x^2+2y\right)\)
\(=-\left(x^2-2y\right)\left(x^2+2y\right)\)
\(=-\left(x^4-4y^2\right)\)
\(=-x^4+4y^2\)
7) \(\left(x+3y\right)\left(x-3y+2\right)\)
\(=x^2-3xy+2x+3xy-9y^2+6y\)
\(=x^2+2x-9y^2+6y\)
8) \(\left(x+2y\right)\left(x-2y+3\right)\)
\(=x^2-2xy+3x+2xy-4y^2+6y\)
\(=x^2+3x-5y^2+6y\)
9) \(\left(x^2-xy+y^2\right)\left(x+y\right)\)
\(=x^3+y^3\)
10) \(\left(x^2-xy+y^2\right)\left(x+y\right)\)
\(=x^3+y^3\)
Đúng 1
Bình luận (0)
Bài 16:
a) \(A-B+C\)
\(=\left(5xy^2-4x^2y-6x^2\right)-\left(8x^2y-4xy^2+3y^2\right)+\left(-2xy^2+3x^2y+5x^2\right)\)
\(=5xy^2-4x^2y-6x^2-8x^2y+4xy^2-3y^2-2xy^2+3x^2y+5x^2\)
\(=\left(5xy^2+4xy^2-2xy^2\right)-\left(4x^2y+8x^2y-3x^2y\right)-\left(6x^2-5x^2\right)-3y^2\)
\(=7xy^2-9x^2y-x^2-3y^2\)
b) \(2\left(A+B\right)+C\)
\(=2\cdot\left(5xy^2-4x^2y-6x^2+8x^2y-4xy^2+3y^2\right)+\left(-2xy^2+3x^2y+5x^2\right)\)
\(=2\cdot\left(xy^2+4x^2y-6x^2+3y^2\right)-2xy^2+3x^2y+5x^2\)
\(=2xy^2+8x^2y-12x^2+6y^2-2xy^2+3x^2y+5x^2\)
\(=11x^2y-7x^2+6y^2\)
Đúng 1
Bình luận (0)
`#3107.101107`
`K = -x^2 + 10x - 30`
`= -(x^2 - 10x + 30)`
`= -[ (x^2 - 2*x*5 + 5^2) + 5]`
`= -[ (x - 5)^2 + 5]`
`= -(x - 5)^2 - 5`
Vì `-(x - 5)^2 \le 0` `AA` `x`
`=> -(x - 5)^2 - 5 \ge -5` `AA` `x`
Vậy, `K_(\text {max})` là `-5` khi `(x - 5)^2 = 0`
`<=> x - 5 = 0`
`<=> x = 5`
_____
`Q = -25y^2 - 20y - 2`
`= -(25y^2 + 20y + 2)`
`= - [ (5y)^2 + 2*5y*2 + 2^2 - 2]`
`= - [(5y + 2)^2 - 2]`
`= - (5y + 2)^2 + 2`
Vì `-(5y + 2)^2 \le 0` `AA` `y`
`=> -(5y + 2)^2 + 2 \ge 2` `AA` `y`
Vậy, `Q_(\text {max})` là `2` khi `(5y + 2)^2 = 0`
`<=> 5y + 2 = 0`
`<=> 5y = -2`
`<=> y = -2/5.`
Đúng 1
Bình luận (0)
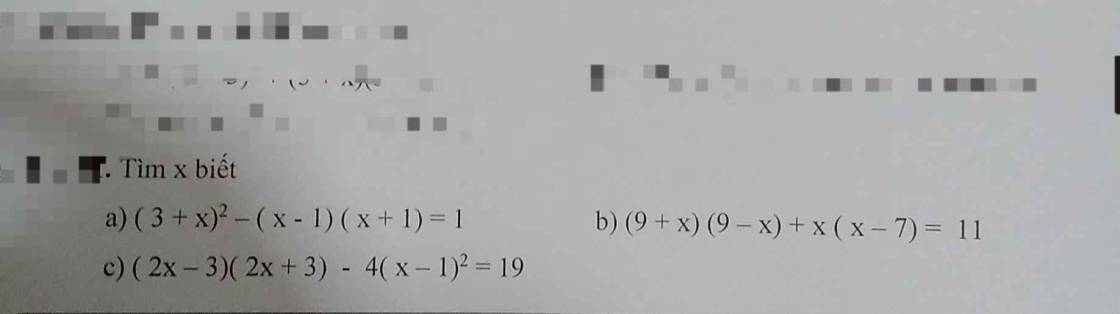 chi tiêttiết
chi tiêttiết
`#3107.101107`
a)
`(3 + x)^2 - (x - 1)(x + 1) = 1`
`<=> 9 + 6x + x^2 - (x^2 - 1) = 1`
`<=> 9 + 6x + x^2 - x^2 + 1 = 1`
`<=> 6x + 10 = 1`
`<=> 6x = 1 - 10`
`<=> 6x = -9`
`<=> x = -3/2`
Vậy, `x = -3/2`
b)
`(9 + x)(9 - x) + x(x - 7) = 11`
`<=> 81 - x^2 + x^2 - 7x = 11`
`<=> 81 - 7x = 11`
`<=> 7x = 70`
`<=> x = 10`
Vậy, `x = 10`
c)
`(2x - 3)(2x + 3) - 4(x - 1)^2 = 19`
`<=> 4x^2 - 9 - 4(x^2 - 2x + 1) = 19`
`<=> 4x^2 - 9 - 4x^2 + 8x - 4 = 19`
`<=> 8x - 13 = 19`
`<=> 8x = 32`
`<=> x = 4`
Vậy, `x = 4.`
______
Sử dụng các hđt:
1. `A^2 - B^2 = (A - B)(A + B)`
2. `(A - B)^2 = A^2 - 2AB + B^2`
3. `(A + B)^2 = A^2 + 2AB + B^2`
d)
Đúng 3
Bình luận (1)
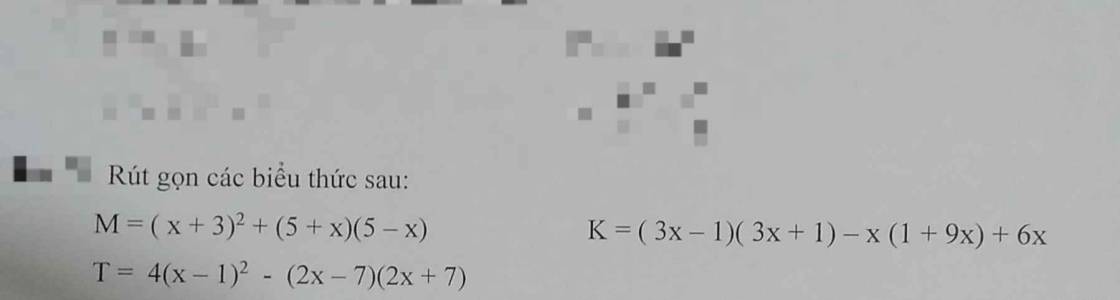 làm xhi tiết
làm xhi tiết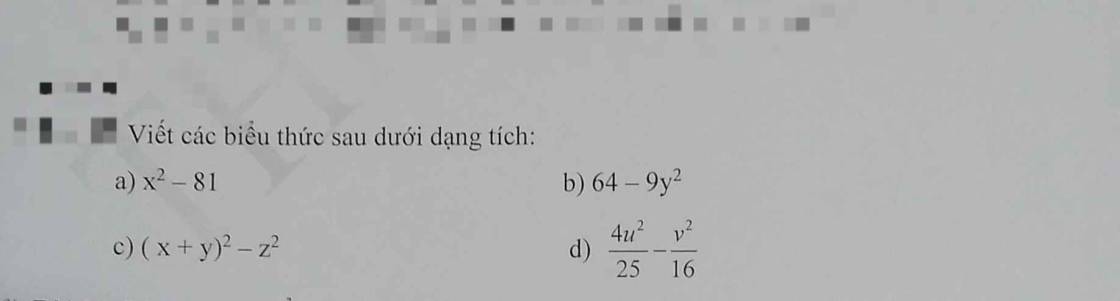 lảm cả 2 bài chi tiết ạ
lảm cả 2 bài chi tiết ạ
(n+2).(n2+3n-1)-n3+2:5
Chắc l: `(n+2)*(n^2+3n-1)-n^3+2⋮5` nhỉ?
Ta có : `(n+2)*(n^2+3n-1)-n^3+2`
`=n*n^2+n*3n-n*1+2*n^2+2*3n-2*1-n^3+2`
`= n^3 +3n^2 -n +2n^2+6n-2-n^3+2`
`= 5n^2 +5n`
`=5n(n+1)`
Vì `5n` luôn chia hết cho `5`
`=> 5n(n+1)⋮5`
Đúng 3
Bình luận (0)
tìm giá trị lớn nhất của e = 6a+3-9a^2
\(E=6a+3-9a^2\)
\(=-\left(9a^2-6a-3\right)\)
\(=-\left(\left(3a\right)^2-2.3a+1-4\right)\)
\(=-\left(3a-1\right)^2+4\)
Vì \(-\left(3a-1\right)^2\le0\forall a\)
\(\Rightarrow E\le4\forall x\)
\(MaxE=4\Leftrightarrow x=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
\(e=6a+3-9a^2\)
\(=-9a^2+6a-1+4\)
\(=-\left(9a^2-6a+1\right)+4\)
\(=-\left[\left(3a\right)^2-2\cdot3a\cdot1+1^2\right]+4\)
\(=-\left(3a-1\right)^2+4\)
Ta thấy: \(\left(3a-1\right)^2\ge0\forall a\)
\(\Rightarrow-\left(3a-1\right)^2\le0\forall a\)
\(\Rightarrow-\left(3a-1\right)^2+4\le4\forall a\)
Dấu \("="\) xảy ra \(\Leftrightarrow3a-1=0\Leftrightarrow a=\dfrac{1}{3}\)
Vậy \(e_{max}=4\) khi \(a=\dfrac{1}{3}.\)
#\(Toru\)
Đúng 0
Bình luận (0)
Cho hai đa thức P=2x-3y và Q= 2x +3y kết quả của PxQ là
\(P\times Q\)
\(=\left(2x+3y\right)\times\left(2x-3y\right)\)
\(=\left(2x\right)^2-\left(3y\right)^2\)
\(=4x^2-9y^2\)
Đúng 3
Bình luận (0)
viết rõ đề ra nha bạn để mọi người hỗ trợ
Đúng 0
Bình luận (0)
\(P.Q=\left(2x-3y\right)\left(2x+3y\right)\)
\(=4x^2-9y^2\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên n để đa thức A chia hết cho đa thức B khi A=x^2.y^4 +2x^3.y^3 và B=x^n.y^3
Ta có: \(A=x^2y^4+2x^3y^3\)
Để A chia hết cho \(B=x^ny^3\) thì:
\(\left\{{}\begin{matrix}2x^3y^3⋮x^ny^3\\x^2y^4⋮x^ny^3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x^3⋮x^n\\x^2⋮x^n\end{matrix}\right.\)
\(\Rightarrow x^0\le x^n\le x^2\)
\(\Rightarrow0\le n\le2\)
Đúng 1
Bình luận (0)
Bài 23:
\(P=x^5y^2-3x^3y+5-x^3y+ax^5y^2=\left(1+a\right)x^5y^2-4x^3y+5\\ Ta.có:x^5y^2\Rightarrow bậc.7\\ -4x^3y\Rightarrow Bậc.4\\ 5:Bậc.0\\ Vậy:P.đa.thức.bậc.4\Leftrightarrow1+a=0\Leftrightarrow a=-1\\ Vậy:a=-1\)
Đúng 1
Bình luận (0)
\(Bài.22:A=x^2-3xy-y^2+1;B=-2x^2+y^2-7xy-5;C=-4+x^2+10xy\\ a,A+B+C=\left(x^2-3xy-y^2+1\right)+\left(-2x^2+y^2-7xy-5\right)+\left(-4+x^2+10xy\right)\\ =\left(x^2-2x^2+x^2\right)+\left(y^2-y^2\right)-\left(7xy+3xy-10xy\right)+1-5-4=-8\)
Vậy: A+B+C không phụ thuộc gì vào biến
\(b,C+A-B=0\\ \Leftrightarrow C=B-A=\left(-2x^2+y^2-7xy-5\right)-\left(x^2-3xy-y^2+1\right)\\ =\left(-2x^2-x^2\right)+\left(y^2+y^2\right)-\left(7xy-3xy\right)-\left(5+1\right)\\ =-3x^2+2y^2-4xy-6\)
Đúng 0
Bình luận (0)
Bài 20:
Bậc của đơn thức là 25
<=> (n+2)+1+3+2 + (n-1)+4=25
<=> 2n+11=25
<=>2n=25-11
<=>2n=14
<=>n=14:2=7
Vậy n=7
Đúng 0
Bình luận (0)