ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
Ta có: \(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{(\sqrt{x}+3)\left(\sqrt{x}-3\right)}-\dfrac{x-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\dfrac{-\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)^2}\)  \(=\left[\dfrac{x-3\sqrt{x}-x+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right].-\left(\sqrt{x}-3\right)\)

  \(=\dfrac{2-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.-\left(\sqrt{x}-3\right)\)

\(=\dfrac{3\sqrt{x}-2}{\sqrt{x}+3}\)

Vậy với \(x\ge0;x\ne9\) thì \(A=\dfrac{3\sqrt{x}-2}{\sqrt{x}+3}\)

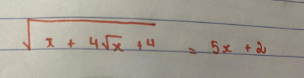
`\sqrt{x + 4\sqrt{x} + 4} = 5x + 2 (x >= 0)`

`<=> \sqrt{(\sqrt{x} + 2)^2} = 5x + 2`

`<=> |\sqrt{x} + 2| = 5x + 2`

`<=> \sqrt{x} + 2 = 5x + 2`

`<=> \sqrt{x} - 5x = 0`

`<=> \sqrt{x}(1 - 5\sqrt{x}) = 0`

`<=> \sqrt{x} = 0` hoặc `1 - 5\sqrt{x} = 0`

`<=> x = 0` hoặc `\sqrt{x} = 1/5`

`<=> x = 0(`tm`)` hoặc `x = 1/25(`tm`)`

Vậy `S = {0 ; 1/25}`

`a)`

`C = (3x + \sqrt{9x} - 3)/(x + \sqrt{x} - 2) - (\sqrt{x}+1)/(\sqrt{x} + 2) - (\sqrt{x} - 2)/(\sqrt{x} - 1)`

`(x >= 0 ; x` $\neq$ `1)`

`C = (3x + 3\sqrt{x} - 3)/((\sqrt{x} - 1)(\sqrt{x} + 2)) - ((\sqrt{x} + 1)(\sqrt{x} - 1))/((\sqrt{x}- 1)(\sqrt{x} + 2)) - ((\sqrt{x} - 2)(\sqrt{x} + 2))/((\sqrt{x} - 1)(\sqrt{x} + 2))`

`C = (3x + 3\sqrt{x} - 3 - x + 1 - x + 4)/((\sqrt{x} - 1)(\sqrt{x} + 2))`

`C = (3x + 3\sqrt{x} - 2x + 2)/((\sqrt{x} - 1)(\sqrt{x} + 2))`

`C = (x + 3\sqrt{x} + 2)/((\sqrt{x} - 1)(\sqrt{x} + 2))`

`C = ((\sqrt{x} + 1)(\sqrt{x} + 2))/((\sqrt{x} - 1)(\sqrt{x} + 2))`

`C = (\sqrt{x} + 1)/(\sqrt{x} - 1)`

`b)`

`x = 3 + 2\sqrt{2} = 2 + 2\sqrt{2} + 1 = (\sqrt{2} + 1)^2`

`=> \sqrt{x} = \sqrt{(\sqrt{2} + 1)^2} = \sqrt{2} + 1`

`C = (\sqrt{2} + 1 + 1)/(\sqrt{2} - 1 + 1)`

`C = (\sqrt{2} + 2)/(\sqrt{2})`

`C = 1 + \sqrt{2}`

`T = \sqrt{2+\sqrt{3}} . \sqrt{2+\sqrt{2+\sqrt{3}}} . \sqrt{2 - \sqrt{2+\sqrt{3}}}`

`T = \sqrt{2+\sqrt{3}} . \sqrt{(2+\sqrt{2+\sqrt{3}})(2 - \sqrt{2} + \sqrt{3})}`

`T = \sqrt{2+\sqrt{3}} . \sqrt{4 - (2 + \sqrt{3})^2}`

`T = \sqrt{2+\sqrt{3}} . \sqrt{4 - |2 + \sqrt{3}|}`

`T = \sqrt{2 + \sqrt{3}} . \sqrt{4 - 2 - \sqrt{3}}`

`T = \sqrt{2 + \sqrt{3}} . \sqrt{2 - \sqrt{3}}`

`T = \sqrt{(2 + \sqrt{3})(2 - \sqrt{3})}`

`T = \sqrt{4 - 3}`

`T = \sqrt{1} = 1`