Số tam giác có thể tạo ra  từ \(144\) đỉnh là:

\(C^3_{144}=\dfrac{144!}{3!\left(144-3\right)!}=\dfrac{144.143.142}{3.2.1}=487344\left(cách\right)\)

Một tam giác đều có các đỉnh cách đều nhau trên đa giác đều. Với đa giác \(144\) cạnh, số tam giác đều có thể tạo thành là:

\(\dfrac{144}{3}=48\left(tam.giác\right)\)

Số tam giác không đều là :

\(487344-48=487296\left(tam.giác\right)\)

Xác xuất rút câu hỏi lý thuyết khó là:

P= 8/50=4/25=0,16

Theo đề bài ta có :

- Tỉ lệ mắc bệnh : \(P\left(M\right)=22\%=0,22\)

- Tỉ lệ không mắc bệnh : \(P\left(M'\right)=1-P\left(M\right)=1-0,22=0,78=78\%\)

- Xác suất test dương tính khi không mắc bệnh \(P\left(+|M'\right)=10\%=0,1\)

- Xác suất mắc bệnh khi test dương tính \(P\left(M|+\right)=70\%=0,7\)

Câu 26 :

Xác suất test cho kết quả chính xác khi một người không mắc bệnh nghĩa là test cho kết quả âm tính khi người đó thực sự không mắc bệnh :

\(P\left(-|M'\right)=1-P\left(+|M'\right)=1-0,1=0,9=90\%\Rightarrow Chọn.D\)

Câu 27 :

Gọi \(P\left(+|M\right)\) là xác suất test cho kết quả dương tính khi một người thực sự mắc bệnh

Ta sử dụng công thức Bayes : 

\(P\left(M|+\right)=\dfrac{P\left(+|M\right).P\left(M\right)}{P\left(+\right)}\left(1\right)\)

Xác suất tổng thể nhận được kết quả dương tính: 

\(P\left(+\right)=P\left(+|M\right).P\left(M\right)+P\left(+|M'\right).P\left(M'\right)\left(2\right)\)

Giải \(\left(1\right);\left(2\right)\Rightarrow P\left(+|M\right)=0,8273=82,73\%\Rightarrow Chọn.B\)

Câu 28 :

Xác suất chẩn đoán đúng của test nghĩa là xác suất test cho kết quả đúng, bao gồm: 

- Test dương tính đúng khi người mắc bệnh: \(P\left(+|M\right).P\left(M\right)\)

- Test âm tính đúng khi người không mắc bệnh: \(P\left(-|M'\right).P\left(M'\right)\)

\(\Rightarrow P\left(chẩn.đoán.đúng\right)=P\left(+|M\right).P\left(M\right)+P\left(-|M'\right).P\left(M'\right)\)

\(\Rightarrow P\left(chẩnđoán.đúng\right)=\left(0,8273.0,22\right)+\left(0,9.0,78\right)=0,884=88,4\%\Rightarrow Chọn.A\)

Bài này chắc ko ai cho trong đề thực tế. Vì đơn giản nó chỉ là check các trường hợp có thể xảy ra.

Hộp 1 có x viên bi (x>7) và hộp 2 có 15-x viên

Giả sử hộp 1 có a viên đen \(\left(0< a\le x\right)\) và hộp 2 có b viên đen

Khi đó: \(\dfrac{a.b}{x.\left(15-x\right)}=\dfrac{5}{28}\)

Dẫn tới x hoặc 15-x phải là bội số của 7. Vậy chỉ có \(x=14\) hoặc \(x=8\). Thử lại 2 cái là ra.

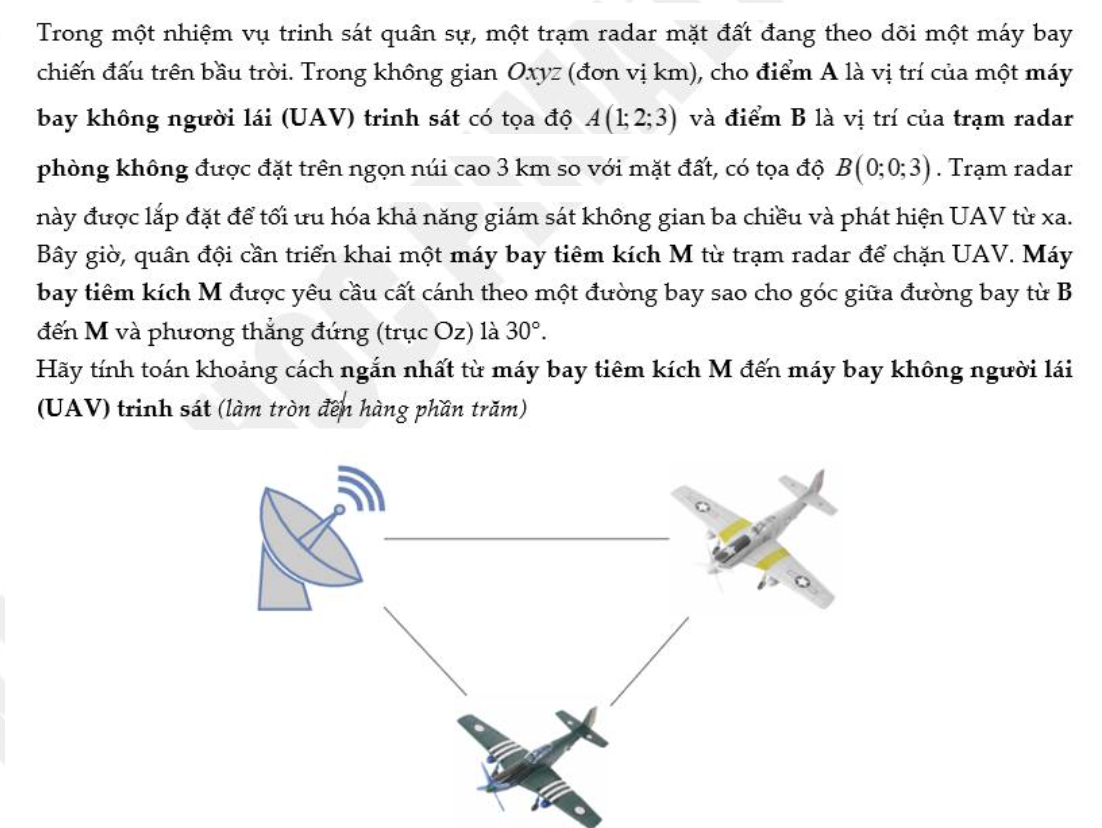
Sao đọc mãi đề bài mình vẫn chưa định hình được máy bay M xuất phát từ điểm nào ta?

Gọi \(M\left(x;y;z\right)\Rightarrow\overrightarrow{BM}=\left(x;y;z-3\right)\)

\(cos\left(\widehat{\overrightarrow{BM};\overrightarrow{Oz}}\right)=cos30^o=\dfrac{\left|z-3\right|}{\sqrt{x^2+y^2+\left(z-3\right)^2}}=\dfrac{\sqrt{3}}{2}\)

\(\Leftrightarrow\dfrac{\left(z-3\right)^2}{x^2+y^2+\left(z-3\right)^2}=\dfrac{3}{4}\)

\(\Leftrightarrow3\left[x^2+y^2+\left(z-3\right)^2\right]=4\left(z-3\right)^2\)

\(\Leftrightarrow3x^2+3y^2=\left(z-3\right)^2\)

\(\Leftrightarrow z-3=\pm\sqrt{3x^2+3y^2}\left(1\right)\)

\(AM=\sqrt{\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2}\)

\(\left(1\right)\Leftrightarrow AM=\sqrt{\left(x-1\right)^2+\left(y-2\right)^2+\left(\sqrt{3x^2+3y^2}\right)^2}=\sqrt{\left(x-1\right)^2+\left(y-2\right)^2+3x^2+3y^2}\)

\(\Leftrightarrow AM=\sqrt{x^2-2x+1+y^2-4y+4+3x^2+3y^2}\)

\(\Leftrightarrow AM=\sqrt{4x^2-2x+4y^2-4y+5}\left(2\right)\)

Đặt \(f\left(x;y\right)=4x^2-2x+4y^2-4y+5\)

\(f'_x=8x-2=0\Leftrightarrow x=\dfrac{1}{4}\)

\(f'_y=8y-4=0\Leftrightarrow y=\dfrac{1}{2}\)

\(\Rightarrow\) Điểm dừng \(M\left(\dfrac{1}{4};\dfrac{1}{2};z\right)\)

\(\left(1\right)\Rightarrow z=\pm\dfrac{\sqrt{15}}{3}+3\Rightarrow M\left(\dfrac{1}{4};\dfrac{1}{2};\pm\dfrac{\sqrt{15}}{4}+3\right)\)

\(f''_{xx}=8;f''_{yy}=8;f''_{xy}=0\)

Ma trận Hessian:\(H=\left[\begin{matrix}8&0\\0&8\end{matrix}\right]\) \(\Rightarrow\left\{{}\begin{matrix}H_1=8>0\\H_2=64-0=64>0\end{matrix}\right.\)

\(\Rightarrow M\left(\dfrac{1}{4};\dfrac{1}{2};\pm\dfrac{\sqrt{15}}{4}+3\right)\) là điểm cực tiểu của \(f\left(x;y\right)\)

\(\left(2\right)\Rightarrow AM\left(min\right)=\sqrt{4\left(\dfrac{1}{4}\right)^2-2\left(\dfrac{1}{4}\right)+4\left(\dfrac{1}{2}\right)^2+5}=\dfrac{\sqrt{15}}{2}\approx1,94\left(km\right)\)

Vậy \(AM=1,94\left(km\right)\) thỏa mãn đề bài

À, tại có đoạn nó ghu "góc đường bay từ B đến M..." nên cứ nghĩ là B ko trùng M

Thay vì ghi khó hiểu như trên, người ta ghi đề là "máy bay tiêm kích xuất phát từ B theo 1 đường thẳng hợp với phương trục Oz 1 góc 30 độ" có phải đỡ rối não ko.

Gọi \(A_1\) là biến cố nhân viên đó là nữ

\(A_2\) là biến cố nhân viên đó là nam

\(A_1;A_2\) tạo thành nhóm biến cố đầy đủ.

\(B\) là biến cố "nhân viên đó có mua bảo hiểm"

Ta có \(P\left(A_1\right)=0,45\) ; \(P\left(A_2\right)=0,55\); \(P\left(B|A_1\right)=0,07\) ; \(P\left(B|A_2\right)=0,05\)

\(P\left(B\right)=0,45.0,07+0,55.0,05=0,059\)

\(P\left(A_2|B\right)=\dfrac{P\left(A_2\right).P\left(B|A_2\right)}{P\left(B\right)}=\dfrac{0,55.0,05}{0,059}=\dfrac{55}{118}\)

Gọi:

- \(P\left(X\right)=0,45\) là xác suất một nhân viên là nữ.

- \(P\left(Y\right)=1-P\left(X\right)=1-0,45=0,55\) là xác suất một nhân viên là nam.

- \(P\left(M\right)\) là xác suất một nhân viên ngẫu nhiên có mua bảo hiểm nhân thọ

- \(P\left(M|X\right)=0,07\) là xác suất mua bảo hiểm nhân thọ nếu nhân viên là nữ.

- \(P\left(M|Y\right)=0,05\) là xác suất mua bảo hiểm nhân thọ nếu nhân viên là nam.

a) Áp dụng công thức xác suất toàn phần ta có xác suất một nhân viên ngẫu nhiên có mua bảo hiểm nhân thọ là

\(P\left(M\right)=P\left(M|X\right)\cdot P\left(X\right)+P\left(M|Y\right)\cdot P\left(Y\right)\) 

\(=0,07\cdot0,45+0,05\cdot0,55=0,059\)

b) Áp dụng công thức Bayes ta có xác suất nhân viên là nam khi biết đã mua bảo hiểm nhân thọ là

\(P\left(Y|M\right)=\dfrac{P\left(M|Y\right)\cdot P\left(Y\right)}{P\left(M\right)}=\dfrac{0,05\cdot0,55}{0,059}=\dfrac{55}{118}\)

Bài này cũng vậy, đọc đề nhưng ko hiểu được người ta muốn nói gì?

- Cửa quay, nhưng trục quay của mỗi cánh nằm ở đâu? Bản lề cánh hay nằm giữa cánh (rất nhiều của xoay có trục nằm giữa cánh cửa, cánh cửa sẽ xoay tròn)

- Hai cánh cửa vốn coi như là 2 phần mặt phẳng, vậy khoảng cách giữa 2 cánh cửa (khi chúng ko song song nhau) là muốn nói đến khoảng cách nào? Hai cánh cửa có vô số điểm, lấy điểm nào làm chuẩn để đo khoảng cách (khi nó ko song song nhau)? Thực sự là "khoảng cách giữa 2 cánh cửa" là 1 điều gì đó ko thể giải thích được

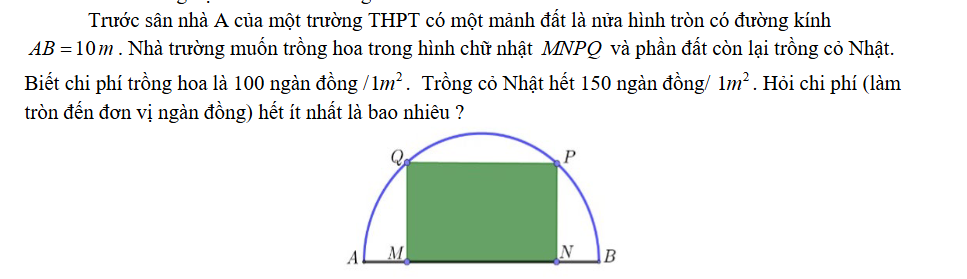
Bán kính \(r=\dfrac{AB}{2}=5\left(m\right)\)

Diện tích nửa hình tròn \(S=\dfrac{1}{2}\pi r^2=\dfrac{25\pi}{2}\left(m^2\right)\)

Đặt \(MN=x\left(0< x< 10\right);MQ-y\)

\(MNPQ\) là hình chữ nhật nội tiếp nửa đường tròn, ta có:

\(OM=\dfrac{x}{2};OQ=y\)

Áp dụng Pitago cho tam giác vuông \(OMQ:\dfrac{x^2}{4}+y^2=25\)

\(\Rightarrow y=\sqrt{25-\dfrac{x^2}{4}}\)

\(S_{MNPQ}=xy=x\sqrt{25-\dfrac{x^2}{4}}\left(m^2\right)\)

\(S_{cỏ}=\dfrac{25\pi}{2}-xy\)

Tổng chi phí: 

\(C=C_{hoa}+C_{cỏ}=100000xy+150000\left[\dfrac{25\pi}{2}-xy\right]=1875000\pi-50000xy\)

Để \(C_{min}\Rightarrow xy\left(max\right)\)

Áp dụng bất đẳng thức Cauchuy cho \(\dfrac{x^2}{4};25-\dfrac{x^2}{4}\)

\(\dfrac{x^2}{4}+\left(25-\dfrac{x^2}{4}\right)\ge2\sqrt{\dfrac{x^2}{4}.\left(25-\dfrac{x^2}{4}\right)}\)

\(\Rightarrow25\ge x\sqrt{25-\dfrac{x^2}{4}}=xy\)

Dấu"=" xảy ra khi \(\dfrac{x^2}{4}=25-\dfrac{x^2}{4}\Rightarrow x=5\sqrt{2}\)

\(\Rightarrow y=\sqrt{25-\dfrac{50}{4}}=\dfrac{5\sqrt{2}}{2}\)

\(\Rightarrow xy=5\sqrt{2}.\dfrac{5\sqrt{2}}{2}=25\)

\(\Rightarrow C_{min}=1875000\pi-50000xy\approx4637500\approx4638000\left(đồng\right)\)