Giúp mik với mn đang cần gấp lắm vì 17h là mik phải có bài r nên giúp mik với!!!
( lm hộ mik bài 2 nha
Hình lăng trụ đứng. Hình chóp đều.
viết lại đi lắn nót vào mới đọc được và hiểu được để mà trả lời chứ viết rõ chữ vào đừng viết tắt
Giúp mik với mn vì bây h mik đang cần gấp lắm 17h là mik phải có bài r nên giúp mik với mn!!!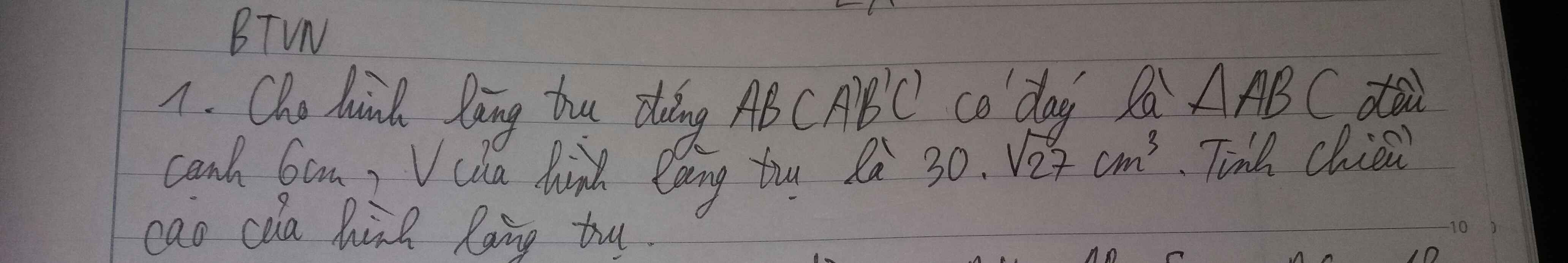
Ánh sáng yếu lắm , với cả chữ hơi khó đọc , hay viết tắt , nếu chứ khó đọc thì hãy viết mực xanh nhìn sáng với cả dễ đọc hơn nhiều đó bn .viết lại đi nếu biết mik trả lời cho nha okay !
Đúng 0
Bình luận (0)
dễ nhưng ko bit làm
Cho hình chóp SABCD có ABCD là hình bình hàng tâm O. Gọi M,N,P lần lượt là các điểm thuộc đoạn AB, AC, SO ( M không trùng với A và B, N không trùng với B và C, P không trùng với S và O).
a. Tìm giao điểm của (MNP) với các đoạn thẳng chứa các cạnh của hình chóp đã cho.
b. Suy ra thiết diện tạo bởi ( MNP) và hình chóp SABCD.
Mọi ng giúp e với
Cho hình hộp chữ nhật ABCD.A’B’C’D’.
a) Chứng minh đường thẳng AD song song với mặt phẳng (A’B’C’D’).
b) Tính thể tích của hình hộp chữ nhật ABCD.A’B’C’D. Biết AB = 3cm, AC = 5cm, AA’ = 2cm.
Giup mik vs
a, Xét mp(AA'D'D) của hình hộp chữ nhật ABCD.A'B'C'D' ta có:
\(AD\text{//}A'D'\) (theo tính chất của hình chữ nhật)
Mà \(A'D'\subset mp\left(A'B'C'D'\right)\) nên \(AD\text{//}mp\left(A'B'C'D'\right)\) (đpcm)
b, Áp dụng định lý Pytago cho ABC vuông tại B ta có:
\(BC=\sqrt{AC^2-AB^2}=\sqrt{5^2-3^3}=4\left(cm\right)\)
Thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là:
\(V=a.b.c=AB.BC.AA'=3.4.2=24\left(cm^3\right)\)
Đúng 0
Bình luận (0)
Giải:
a) Vì đường thẳng AD song song với một trong bốn cạnh của mặt phẳng (A'B'C'D')
Nên đường thẳng AD song song với mặt phẳng (A'B'C'D')
Hay \(AD//mp\left(A'B'C'D'\right)\)
b) Thể tích hình hộp chữ nhật ABCD.A'B'C'D' là:
\(S_{ABCD.A'B'C'D'}=a.b.c=AB.AC.AA'=3.5.2=30\left(cm^3\right)\)
Vậy ...
Đúng 0
Bình luận (0)
a)
AD// mp \(\left(A'B'C'D'\right)\), vì có:
AD \(\notin mp\left(A'B'C'D'\right)\)
AD//A'D'
=>AD// mp \(\left(A'B'C'D'\right)\)( đpcm)
b)
Xét \(\Delta ABC\), có:
Góc ABC = 90o ( tứ giác ABCD là hình chữ nhật)
=> \(\Delta ABC\)\(\perp B\)
Theo định lý Py-ta-go, ta có:
\(AC^2=AB^2+BC^2\)
\(\Rightarrow BC=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(\Rightarrow V_{ABCD.A'B'C'D'}=3.4.2=24\left(cm^3\right)\)
Đúng 0
Bình luận (2)
Xem thêm câu trả lời
Cho hình lăng trụ đứng. ABC,A'B'C' đáy tam giác ABC có AB=6cm,BC=8cm,AC=10cm và chiều cao của lăng trụ là 12cm a)chứng tỏ A'B'C' là tam giác vuông b)Tính diện tích xung quanh,toàn phần của hình lăng trụ c)Tính thể tích lăng trụ
Một bóng đèn huỳnh quang dài 1,2m, đường kính của đường tròn đáy là 4cm, được đặt khít vào 1 hộp ống giấy cứng dạng hình hộp. Tính diện tích phần giấy cứng dùng để làm 1 hộp. ( hộp hở 2 đầ, không tính lề và mép dán)
Bài 1: Cho hình chóp tam giác S.ABC, điểm G là trọng tâm của tam giác SBC. Gọi K là trung điểm của SA. hãy xác định giao điểm của đường thẳng KG và mặt phẳng (ABC)
giúp e với. mai e thi rồi :'<
Đúng 0
Bình luận (0)
Tính thể tích của một hình lập phương, biết diện tích toàn phần của nó là 216 cm2
Lời giải:
Gọi độ dài cạnh của hình lập phương là $a$ ( $a>0$)
Diện tích một mặt là: \(S=a^2\)
\(\Rightarrow S_{\text{toàn phần}}=6a^2=216\Rightarrow a^2=36\Rightarrow a=6\) (cm)
Vậy thể tích của hình lập phương là:
\(V=a^3=6^3=216( cm ^3)\)
Đúng 0
Bình luận (0)
cho hình lăng trụ đứng ABCD.ABCD, đáy ABCD là hìh thang vuông có góc A góc D 90o, ABBCAA4cm, góc C bằng 60o
a) Chứng minh mp(ABBA) ⊥mp(ADDA)
b) Tính diện tích toàn phần, thể tích của hình lăng trụ đứng
ĐS: b) Sxqapprox 34,92 (cm2)
V approx69,20 (cm3)
giúp mình với nhaa
Đọc tiếp
cho hình lăng trụ đứng ABCD.A'B'C'D', đáy ABCD là hìh thang vuông có góc A= góc D =90o, AB=BC=AA'=4cm, góc C bằng 60o
a) Chứng minh mp(ABB'A') ⊥mp(ADD'A')
b) Tính diện tích toàn phần, thể tích của hình lăng trụ đứng
ĐS: b) Sxq\(\approx\) 34,92 (cm2)
V \(\approx\)69,20 (cm3)
giúp mình với nhaa
Cho hình chữ nhật ABCD có AB=12cm, BC=9cm.Gọi H là chân đường vuông góc kẻ từ A xuống BD.
a/ Chứng minh: tam giác AHB đồng dạng với tam giác BCD.
b/ Tính độ dài đoạn thẳng AH.
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó: ΔAHB\(\sim\)ΔBCD
b: \(BD=\sqrt{12^2+9^2}=15\left(cm\right)\)
\(AH=\dfrac{12\cdot9}{15}=7.2\left(cm\right)\)
Đúng 0
Bình luận (0)



