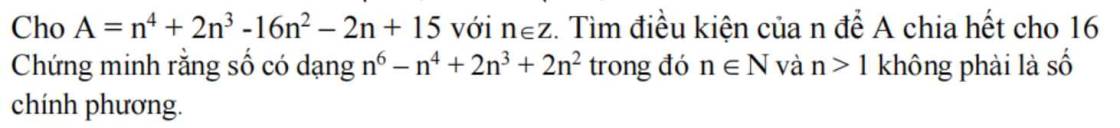Câu 1:
Ở câu này, trước khi tìm lời giải bài toán, ta nên thử vài số nguyên trước để có định hướng làm bài.
- Với \(n\in Z;n\in\left[-5,9\right]\), ta có kết quả sau:
| n | A |
| -5 | 0 |
| -4 | -105 |
| -3 | -96 |
| -2 | -45 |
| -1 | 0 |
| 0 | 15 |
| 1 | 0 |
| 2 | -21 |
| 3 | 0 |
| 4 | 135 |
| 5 | 480 |
| 6 | 1155 |
| 7 | 2304 |
| 8 | 4095 |
| 9 | 6720 |
Để ý rằng, với n lẻ và n thuộc khoảng trên thì A chia hết cho 16.
Vậy ta sẽ cố chứng minh rằng, khi n lẻ thì A chia hết cho 16 và ngược lại.
Tiếp tục quan sát, ta thấy \(n=-5;-1;1;3\) là các nghiệm của đa thức A.
Do đó, đa thức A có thể viết lại thành: \(A=\left(x+5\right)\left(x+1\right)\left(x-1\right)\left(x-3\right)\)
Với n lẻ thì mỗi nhân tử của A đều chẵn, do đó A sẽ chia hết cho \(2.2.2.2=16\)
(Tương tự với n chẵn).
- Vậy với n lẻ thì A chia hết cho 16
Câu 2: Phân tích \(B=n^6-n^4+2n^3+2n^2\) thành nhân tử, ta được:
\(B=n^2\left(n+1\right)^2\left[\left(n-1\right)^2+1\right]\)
Giả sử B là một số chính phương, khi đó \(\left(n-1\right)^2+1\) cũng phải là một số chính phương.
Đặt \(\left(n-1\right)^2+1=a^2\) \(\Leftrightarrow\left(a+n-1\right)\left(a-n+1\right)=1\)
Giải phương trình ước số trên, ta được: \(a=1;n=1\) (loại vì n>1).
Vậy điều giả sử là sai. Ta có điều phải chứng minh.