Chương III : Thống kê
\(a) \)
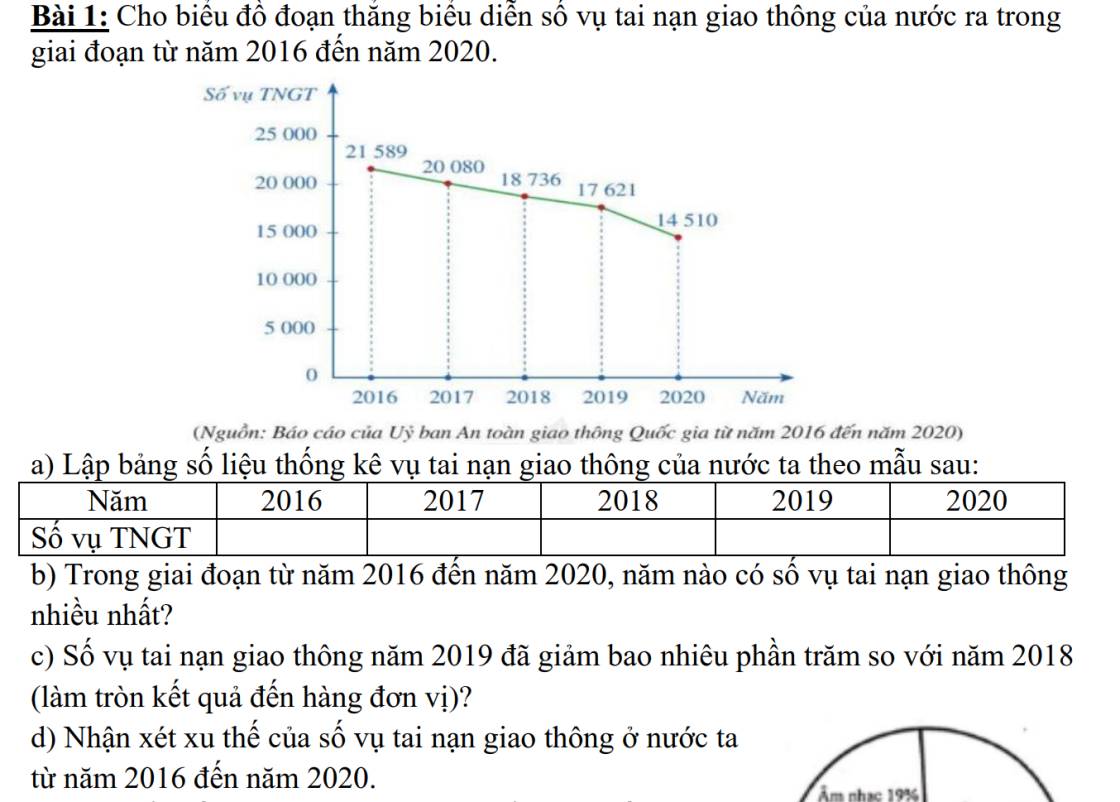
| Năm | 2016 | 2017 | 2018 | 2019 | 2020 |
| Số vụ TNGT | 21 589 | 20 080 | 18 736 | 17 621 | 14 510 |
`b)`
Vì `21\ 589 > 20\ 080>18\ 736> 17\ 621> 14\ 510` nên năm 2016 có số vụ TNGT cao nhất
`c)`
Số vụ tai nạn giao thông năm `2019` đã giảm số phần trăm so với năm `2018` là `:`
`(18 736-17621)/(17621) . 100%~~6,3%`
`d)`
Xu thế của số vụ tai nạn giao thông ở nước ta đang giảm dần
Đúng 2
Bình luận (0)
a) Cho tam giác ABC có góc A bằng 70 độ góc B bằng 30 độ, góc C bằng 80 độ. Sắp xếp các cạnh của ∆ABC theo thứ tự từ nhỏ đến lớn.
b) Cho đoạn thẳng MN có độ dài bằng 6cm. Vẽ đường trung trực d của đoạn thẳng MN.
a: góc B<góc A<góc C
=>AC<BC<AB
b:

Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH. Kẻ HM vuông góc AB tại M; HN vuông góc AC tại N.
1. Chứng minh: BH = CH.
2. Chứng minh: AMN cân
3. Gọi P là giao điểm của MH với AC, Q là giao điểm của NH với AB, I là trung điểm của PQ. Chứng minh ba điểm N; H; I thẳng hàng.
1: ΔABC cân tại A
mà AH là đường cao
nen H là trung điểm của BC và AH là phân giác của góc BAC
=>HB=HC
2: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>AM=AN
=>ΔAMN cân tại A
Đúng 0
Bình luận (0)
viết ngẫu nhiên 1 số tự nhiên có 2 chữ sô
a) tính số kết quả có thể xảy ra đối với số tự nhiên được viết ra
b) tính xát suất của mỗi biến cố sau
A:"số tự nhiên được viết ra là bình phương của 1 số tự nhiên"
B:"số tự nhiên được viết ra là bôi của 12"
C:"số tự nhiên được viết ra là ước của 100"
a: n(omega)=99-10+1=90
b: A={16;25;36;49;64;81}
=>n(A)=6
=>P(A)=6/90=1/15
B={12;24;36;48;60;72;84;96}
=>n(B)=8
=>P(B)=8/90=4/45
C={10;20;25;50}
=>P(C)=4/90=2/45
Đúng 0
Bình luận (0)
Một hộp có 100 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1;2;3;...;99;100, hai thẻ khác nhau thì ghi hai số khác nhauRút ngẫu nhiên một thẻ trong hộp. Tính xát suất của các biến cố sau:a) biến cố A Số xuất hiện trên thẻ được rút ra là số có một chữ số .b) biến cố B Số xuất hiện trên thẻ được rút ra là số chia hết cho 7c) biến cố C Số xuất hiện trên thẻ được rút ra là số nguyên tốd) biến cố D Số xuất hiện trên thẻ được rút ra là số các chữ số bằng 10
Đọc tiếp
Một hộp có 100 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1;2;3;...;99;100, hai thẻ khác nhau thì ghi hai số khác nhau
Rút ngẫu nhiên một thẻ trong hộp. Tính xát suất của các biến cố sau:
a) biến cố A "Số xuất hiện trên thẻ được rút ra là số có một chữ số ".
b) biến cố B "Số xuất hiện trên thẻ được rút ra là số chia hết cho 7"
c) biến cố C "Số xuất hiện trên thẻ được rút ra là số nguyên tố"
d) biến cố D "Số xuất hiện trên thẻ được rút ra là số các chữ số bằng 10"
tung 1 đồng xu cân đối đồng chất 20 lần, trong đó có 12 lần xuất hiện mặt ngửa. Tính xát suất của biến cố" Tung được mặt sấp"?
A. 8
B. 12
C. \(\dfrac{3}{5}\)
D. \(\dfrac{1}{5}\)
Vì tung đồng xu 20 lần mà có 12 lần mặt ngửa nên có 8 mặt sấp.
Xác suất của biến cố ''Tung được mặt sấp'' là: \(\dfrac{8}{20}=\dfrac{2}{5}\)
Đáp số: `2/5`.
Do đó: không có đáp án nào đúng cả.
Đúng 2
Bình luận (0)
Bài 1. Điều tra về cân nặng (kg) của các bạn học sinh lớp 7A, giáo viên ghi lại trong bảngsau: 394145424245424541424245394541423942424145424142424245414545a) Hoànthànhbảng sốliệuthống kêcânnặng của30bạnhọcsinh lớp7Atheomẫusau:Cânnặng(kg)39414245Sốhọcsinh b) Tính tổng số bạn học sinh lớp 7A c) Tính tỉ số phần trăm của số bạn cân năng trên 42kg so với cả lớp.
Đọc tiếp
Bài 1. Điều tra về cân nặng (kg) của các bạn học sinh lớp 7A, giáo viên ghi lại trong bảngsau:
39 | 41 | 45 | 42 | 42 | 45 | 42 | 45 | 41 | 42 |
42 | 45 | 39 | 45 | 41 | 42 | 39 | 42 | 42 | 41 |
45 | 42 | 41 | 42 | 42 | 42 | 45 | 41 | 45 | 45 |
a) Hoànthànhbảng sốliệuthống kêcânnặng của30bạnhọcsinh lớp7Atheomẫusau:
Cânnặng(kg) | 39 | 41 | 42 | 45 |
Sốhọcsinh |
|
|
|
|
b) Tính tổng số bạn học sinh lớp 7A
c) Tính tỉ số phần trăm của số bạn cân năng trên 42kg so với cả lớp.
Cho tam giác ABC có AB =AC góc ACB bằng 50°. M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho AM = MD a) Chứng minh AM là tia phân giác của góc BAC b)tính số đo các góc của tam giác ABC c) Chứng minh AB//CD và AB = CD
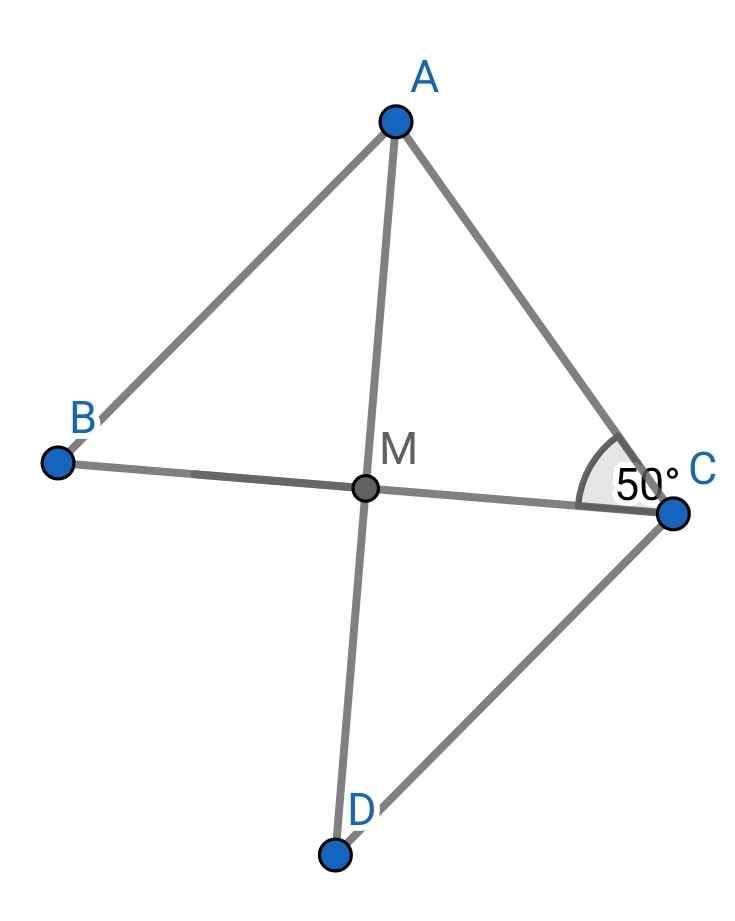
a) Xét tam giác ABM và tam giác ACM có:
AB = AC (gt)
BM = CM (M là trung điểm BC)
AM là cạnh chung
Suy ra tam giác ABM = tam giác ACM (c-c-c)
Suy ra góc BAM = góc CAM (hai góc tương ứng)
Suy ra AM là tia phân giác của góc BAC
b) Tam giác ABC có:
AB = AC (gt)
Suy ra tam giác ABC cân tại A
Suy ra góc ABC = góc ACB = 50⁰
Lại có:
góc ABC + góc ACB + góc BCA = 180⁰ (tổng ba góc trong tam giác ABC)
Suy ra góc BAC = 180⁰ - (góc ABC + góc ACB)
= 180⁰ - (50⁰ + 50⁰)
= 80⁰
c) Xét tam giác ABM và tam giác DCM có:
AM = DM (gt)
BM = CM (M là trung điểm BC)
góc AMB = góc DMC (đối đỉnh)
Suy ra tam giác ABM = tam giác DCM (c-g-c)
Suy ra AB = CD (hai cạnh tương ứng)
Góc ABM = góc DCM (hai góc tương ứng)
Mà góc ABM và góc DCM (so le trong)
Suy ra AB // CD
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B = 60 độ; AB=a:
a) vẽ hình, tính góc C.
b) tính BC; AC theo a.
c) tính các tỉ số lượng giác của góc 60 độ và góc 30 độ.
a: góc C=90-60=30 độ
b: Xét ΔABC vuông tại A có
\(\cos B=\dfrac{AB}{BC}\)
=>BC=2a
=>\(AC=a\sqrt{3}\)
c: \(\sin30=\cos60=\dfrac{1}{2}\)
\(\sin60=\cos30=\dfrac{\sqrt{3}}{2}\)
\(\tan30=\cot60=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
\(\tan60=\cot30=\sqrt{3}\)
Đúng 1
Bình luận (0)