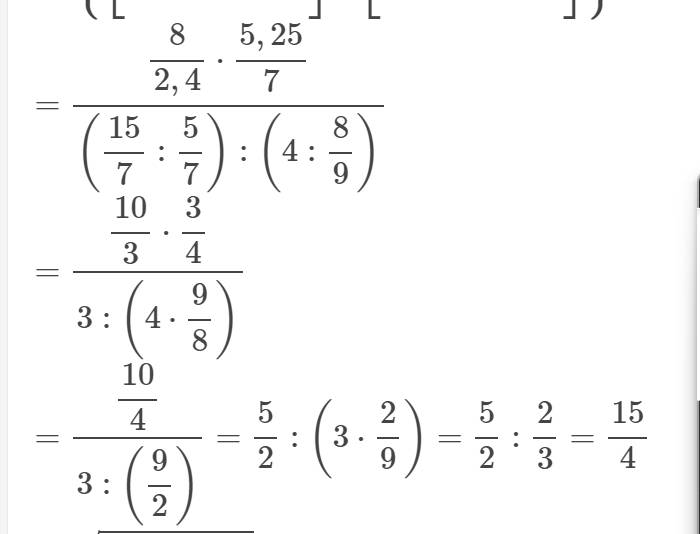Chương I : Số hữu tỉ. Số thực

a: \(A=\dfrac{1-\dfrac{1}{\sqrt{49}}+\dfrac{1}{49}-\dfrac{1}{\left(7\sqrt{7}\right)^2}}{\dfrac{\sqrt{64}}{2}-\dfrac{4}{7}+\left(\dfrac{2}{7}\right)^2-\dfrac{4}{343}}\)

\(=\dfrac{1-\dfrac{1}{7}+\dfrac{1}{49}-\dfrac{1}{343}}{4-\dfrac{4}{7}+\dfrac{4}{49}-\dfrac{4}{343}}\)

\(=\dfrac{1-\dfrac{1}{7}+\dfrac{1}{49}-\dfrac{1}{343}}{4\left(1-\dfrac{1}{7}+\dfrac{1}{49}-\dfrac{1}{343}\right)}=\dfrac{1}{4}\)

b: \(M=1-\dfrac{5}{\sqrt{196}}-\dfrac{5}{\left(2\sqrt{21}\right)^2}-\dfrac{\sqrt{25}}{204}-\dfrac{\left(\sqrt{5}\right)^2}{374}\)

\(=1-\dfrac{5}{14}-\dfrac{5}{84}-\dfrac{5}{204}-\dfrac{5}{374}\)

\(=1-5\left(\dfrac{1}{14}+\dfrac{1}{84}+\dfrac{1}{204}+\dfrac{1}{374}\right)\)

\(=1-5\left(\dfrac{1}{2\cdot7}+\dfrac{1}{7\cdot12}+\dfrac{1}{12\cdot17}+\dfrac{1}{17\cdot22}\right)\)

\(=1-\left(\dfrac{5}{2\cdot7}+\dfrac{5}{7\cdot12}+\dfrac{5}{12\cdot17}+\dfrac{5}{17\cdot22}\right)\)

\(=1-\left(\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{12}+\dfrac{1}{12}-\dfrac{1}{17}+\dfrac{1}{17}-\dfrac{1}{22}\right)\)

\(=1-\left(\dfrac{1}{2}-\dfrac{1}{22}\right)\)

\(=1-\dfrac{11-1}{22}=1-\dfrac{10}{22}=\dfrac{12}{22}=\dfrac{6}{11}\)

a: Sửa đề: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)

Để A là số nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)

=>\(\sqrt{x}-3+4⋮\sqrt{x}-3\)

=>\(4⋮\sqrt{x}-3\)

=>\(\sqrt{x}-3\in\left\{1;-1;2;-2;4;-4\right\}\)

=>\(\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)

=>\(\sqrt{x}\in\left\{4;2;5;1;7\right\}\)

=>\(x\in\left\{16;4;25;1;49\right\}\)

b: 

a: ĐKXĐ: x>0

Để A là số nguyên thì \(7⋮\sqrt{x}\)

=>\(\sqrt{x}\in\left\{1;7\right\}\)

=>\(x\in\left\{1;49\right\}\)

b: ĐKXĐ: x>1

Để B là số nguyên thì \(3⋮\sqrt{x-1}\)

=>\(\sqrt{x-1}\in\left\{1;3\right\}\)

=>\(x-1\in\left\{1;9\right\}\)

=>\(x\in\left\{2;10\right\}\)

c: ĐKXĐ: x>3

Để C là số nguyên thì \(2⋮\sqrt{x-3}\)

=>\(\sqrt{x-3}\in\left\{1;2\right\}\)

=>\(x-3\in\left\{1;4\right\}\)

=>\(x\in\left\{4;7\right\}\)

Sửa đề:: \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

Thay x=16/9 vào A, ta được:

\(A=\dfrac{\sqrt{\dfrac{16}{9}}+1}{\sqrt{\dfrac{16}{9}}-1}=\dfrac{\dfrac{4}{3}+1}{\dfrac{4}{3}-1}=\dfrac{7}{3}:\dfrac{1}{3}=7\) là số nguyên

Thay x=25/9 vào A, ta được:

\(A=\dfrac{\sqrt{\dfrac{25}{9}}+1}{\sqrt{\dfrac{25}{9}}-1}=\dfrac{\dfrac{5}{3}+1}{\dfrac{5}{3}-1}=\dfrac{8}{3}:\dfrac{2}{3}=4\) là số nguyên

a: \(\left(2x-3\right)^2=\left|3-2x\right|\)

=>\(\left\{{}\begin{matrix}\left|2x-3\right|>=0\\\left(2x-3\right)^2=\left(2x-3\right)\end{matrix}\right.\Leftrightarrow\left(2x-3\right)^2-\left(2x-3\right)=0\)

=>\(\left(2x-3\right)\left(2x-3-1\right)=0\)

=>\(\left(2x-3\right)\left(2x-4\right)=0\)

=>\(\left[{}\begin{matrix}2x-3=0\\2x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\end{matrix}\right.\)

b: \(\left(x-1\right)^2+\left(2x-1\right)^2=0\)

=>\(x^2-2x+1+4x^2-4x+1=0\)

=>\(5x^2-6x+2=0\)

\(\Delta=\left(-6\right)^2-4\cdot5\cdot2=36-20\cdot2=-4< 0\)

=>Phương trình vô nghiệm

c: ĐKXĐ: x>=0

\(x-2\sqrt{x}=0\)

=>\(\sqrt{x}\cdot\sqrt{x}-2\cdot\sqrt{x}=0\)

=>\(\sqrt{x}\left(\sqrt{x}-2\right)=0\)

=>\(\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(nhận\right)\end{matrix}\right.\)

d: \(\left(x-1\right)^2+\dfrac{1}{7}=0\)

mà \(\left(x-1\right)^2+\dfrac{1}{7}>=\dfrac{1}{7}>0\forall x\)

nên \(x\in\varnothing\)

`#3107.101107`

`1.`

`a,`

`(2x - 3)^2 = |3 - 2x|`

`=> (2x - 3)^2 = |2x - 3|`

`=>`\(\left[{}\begin{matrix}2x-3=\left(2x-3\right)^2\\2x-3=-\left(2x-3\right)^2\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}2x-3-\left(2x-3\right)^2=0\\2x-3+\left(2x-3\right)^2=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}\left(2x-3\right)\left(1-2x+3\right)=0\\\left(2x-3\right)\left(1+2x-3\right)=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}2x-3=0\\4-2x=0\\2x-2=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=2\\x=1\end{matrix}\right.\)

Vậy, `x \in {3/2; 2; 1}`

`b,`

`(x - 1)^2 + (2x - 1)^2 = 0`

`=>`\(\left[{}\begin{matrix}\left(x-1\right)^2=0\\\left(2x-1\right)^2=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x-1=0\\2x-1=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)

Vậy, `x \in {1; 1/2}`

`c,`

`5 - x^2 = 1`

`=> x^2 = 4`

`=> x^2 = (+-2)^2`

`=> x = +-2`

Vậy, `x \in {-2; 2}`

`d,`

`x - 2\sqrt{x} = 0`

`=> x^2 - (2\sqrt{x})^2 = 0`

`=> x^2 - 4x = 0`

`=> x(x - 4) = 0`

`=>`\(\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\)

`=>`\(\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

Vậy, `x \in {0; 4}`

`g,`

`(x - 1) + 1/7 = 0`

`=> x - 1 + 1/7 = 0`

`=> x - 6/7 = 0`

`=> x = 6/7`

Vậy, `x = 6/7.`

a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)

\(\left(b-1\right)^{2024}>=0\forall b\)

Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)

Thay a=-1 và b=1 vào P, ta được:

\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)

\(\dfrac{2^3}{3\cdot5}+\dfrac{2^3}{5\cdot7}+...+\dfrac{2^3}{101\cdot103}\)

\(=2^2\left(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{101\cdot103}\right)\)

\(=4\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{101}-\dfrac{1}{103}\right)\)

\(=4\cdot\left(\dfrac{1}{3}-\dfrac{1}{103}\right)\)

\(=4\cdot\dfrac{100}{309}=\dfrac{400}{309}\)

a: \(\left(2x-y+7\right)^{2022}>=0\forall x,y\)

\(\left|x-1\right|^{2023}>=0\forall x\)

=>\(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}>=0\forall x,y\)

mà \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}< =0\forall x,y\)

nên \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}=0\)

=>\(\left\{{}\begin{matrix}2x-y+7=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x+7=9\end{matrix}\right.\)

\(P=x^{2023}+\left(y-10\right)^{2023}\)

\(=1^{2023}+\left(9-10\right)^{2023}\)

=1-1

=0

c: \(\left|x-3\right|>=0\forall x\)

=>\(\left|x-3\right|+2>=2\forall x\)

=>\(\left(\left|x-3\right|+2\right)^2>=4\forall x\)

mà \(\left|y+3\right|>=0\forall y\)

nên \(\left(\left|x-3\right|+2\right)^2+\left|y+3\right|>=4\forall x,y\)

=>\(P=\left(\left|x-3\right|+2\right)^2+\left|y-3\right|+2019>=4+2019=2023\forall x,y\)

Dấu '=' xảy ra khi x-3=0 và y-3=0

=>x=3 và y=3

Bài 3:

Giá bán của 1 chiếc túi trong 30 chiếc túi đầu là:

\(150000\left(1+30\%\right)=195000\left(đồng\right)\)

Giá bán của 1 chiếc túi trong 20 chiếc túi sau là:

\(150000\left(1-5\%\right)=142500\left(đồng\right)\)

Số tiền thu được khi bán 30 chiếc túi đầu là:

\(195000\cdot30=5850000\left(đồng\right)\)

Số tiền thu được khi bán 20 chiếc túi sau là:

\(142500\cdot20=2850000\left(đồng\right)\)

Tổng số tiền thu được là:

\(5850000+2850000=8700000\left(đồng\right)\)

Số tiền nhập về là:

\(150000\cdot50=7500000\left(đồng\right)\)

Ta có: 8700000-7500000=1200000(đồng)

=>Cửa hàng lãi được 1200000 đồng

Bài 2:

Giá bán của 1 chiếc laptop trong 70 cái đầu là:

\(8000000\cdot\left(1+30\%\right)=10400000\left(đồng\right)\)

Giá bán của 1 chiếc laptop trong 30 cái sau là:

\(10400000\cdot65\%=6760000\left(đồng\right)\)

Số tiền thu được khi bán 70 cái laptop đầu là:

\(10400000\cdot70=728000000\left(đồng\right)\)

Số tiền thu được khi bán 30 cái laptop sau là:

\(6760000\cdot30=202800000\left(đồng\right)\)

Tổng số tiền thu được là:

\(728000000+202800000=930800000\left(đồng\right)\)

Số tiền nhập về là:

\(8000000\cdot100=800000000\left(đồng\right)\)

Vì 930800000-800000000=130800000 đồng

nên cửa hàng lãi được 130800000 đồng