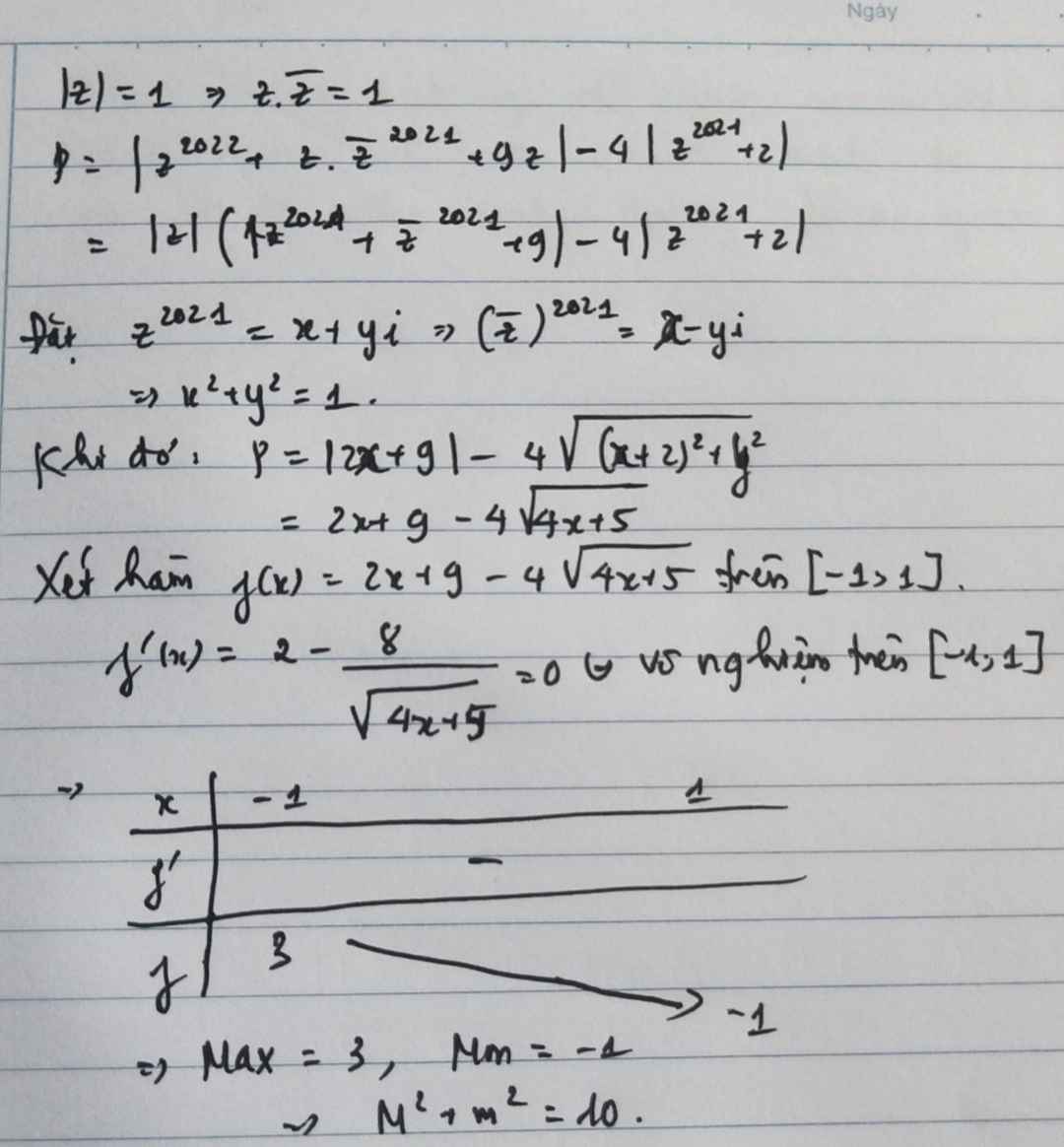Chương 4: SỐ PHỨC
Đặt \(z=x+yi\)
\(\left|z-2+3i\right|=3\Leftrightarrow\left|x+yi-2+3i\right|=3\)
\(\Leftrightarrow\left|x-2+\left(y+3\right)i\right|=3\)
\(\Leftrightarrow\sqrt{\left(x-2\right)^2+\left(y+3\right)^2}=3\)
\(\Leftrightarrow\left(x-2\right)^2+\left(y+3\right)^2=9\)
Đúng 0
Bình luận (0)
các điểm biểu diễn số phức \(z\) cách đều điểm \(I\left(2;4\right)\) một khoảng 2 nên quỹ tích \(z\) là đường tròn tâm \(I\left(2;4\right),R=2\)
Đặt \(M\left(z\right),N\left(1;-2\right)\), bài toán trở thành tìm max min của độ dài đoạn \(MN\)
Do \(IN=\sqrt{37}>2\)
Nên max \(MN=IN+R=\sqrt{37}+2;min\)\(MN=IN-R=\sqrt{37}-2\)
Đúng 2
Bình luận (0)
Cho số phức \(z\) thỏa mãn \(\left|z\right|=1\) và biểu thức \(P=\left|z^{2022}+\left(\overline{z}\right)^{2020}+9z\right|-4\left|z^{2021}+2\right|\). Gọi \(M,m\) là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(P\). Giá trị của \(M^2+m^2\) bằng?
cho các số phức \(z,w\) thỏa mãn \(\left|z\right|=4\) và \(\left|w\right|=5\). Khi \(\left|2x+w-9+12i\right|\) đạt giá trị nhỏ nhất thì \(\left|z-w\right|\) bằng?
Cho hai số phức z_1,z_2 thỏa mãn left|z_1+3+2iright|1 và left|z_2+2-iright|1. Xét các số phức za+bi, (a,bin R) thỏa mãn 2a-b0. Khi biểu thức Tleft|z-z_1right|+left|z-2z_2right| đạt giá trị nhỏ nhất thì giá trị biểu thức Pa^2+b^2 bằng?
Đọc tiếp
Cho hai số phức \(z_1,z_2\) thỏa mãn \(\left|z_1+3+2i\right|=1\) và \(\left|z_2+2-i\right|=1\). Xét các số phức \(z=a+bi\), (\(a,b\in R\)) thỏa mãn \(2a-b=0\). Khi biểu thức \(T=\left|z-z_1\right|+\left|z-2z_2\right|\) đạt giá trị nhỏ nhất thì giá trị biểu thức \(P=a^2+b^2\) bằng?
Có bao nhiêu số phức z thỏa mãn \(\dfrac{z}{z^2+2\overline{z}}\) là số thực và \(\left(z+2\right)\left(\overline{z}+2i\right)\) là số thuần ảo?
Cho \(z_1,z_2\) là hai số phức thoả mãn \(\left|z-4-3i\right|=2\) và \(\left|z_1-z_2\right|=3\). Giá trị lớn nhất của biểu thức \(M=\left|z_1+z_2-2+2i\right|\) là
Tìm tất cả các số phức \(z\) thỏa mãn điều kiện:
\(\left|iz-1-3i\right|.\left|\overline{z}+1+i\right|=\left|z^2+\left(-6+2i\right)z+8-6i\right|\) và \(\dfrac{z-3}{z+2}\) là số thuần ảo.
Cho số phức \(z\) thỏa mãn \(\left|z\right|=1\). Giá trị lớn nhất của biểu thức \(P=\left|1+z\right|+2\left|1-z\right|\) bằng?
Có cách nào chứng minh không cần dùng bất đẳng thức Bunyakovsky không ạ, mình cảm ơn nhiều♥

Có thể đưa về hàm số:
\(AB=2\Rightarrow MB=\sqrt{AB^2-MA^2}=\sqrt{4-MA^2}\)
Đặt \(MA=t\) với \(0\le t\le2\) \(\Rightarrow MB=\sqrt{4-t^2}\)
\(P=MA+2MB=f\left(t\right)=t+2\sqrt{4-t^2}\)
Xét hàm \(f\left(t\right)\) trên \(\left[0;2\right]\)
\(f'\left(t\right)=1-\dfrac{2t}{\sqrt{4-t^2}}=0\Rightarrow2t=\sqrt{4-t^2}\Rightarrow5t^2=4\Rightarrow t=\dfrac{2}{\sqrt{5}}\)
\(f\left(0\right)=4\) ; \(f\left(2\right)=2\) ; \(f\left(\dfrac{2}{\sqrt{5}}\right)=2\sqrt{5}\)
\(\Rightarrow f\left(t\right)_{max}=2\sqrt{5}\Rightarrow P_{max}=2\sqrt{5}\)
Đúng 1
Bình luận (0)
Cho số phức z thỏa mãn left|z-3-4iright|sqrt{5}. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức Pleft|z+2right|^2-left|z-iright|^2. Môđun của số phức wM+mi là?Giải thích cho mình dòng bôi vàng ở dưới ạ, mình cảm ơn nhiều ♥
Đọc tiếp
Cho số phức \(z\) thỏa mãn \(\left|z-3-4i\right|=\sqrt{5}\). Gọi \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P=\left|z+2\right|^2-\left|z-i\right|^2\). Môđun của số phức \(w=M+mi\) là?
Giải thích cho mình dòng bôi vàng ở dưới ạ, mình cảm ơn nhiều ♥

Mọi điểm M biểu diễn z đều phải thỏa mãn 2 điều kiện: vừa thuộc đường tròn (C) vừa thuộc đường thẳng \(\Delta\) (tham số P)
Do đó, M là giao điểm của (C) và \(\Delta\)
Hay tham số P phải thỏa mãn sao cho (C) và \(\Delta\) có ít nhất 1 điểm chung
Hay hệ pt nói trên có nghiệm (thật ra chi tiết đó là thừa, chỉ cần biện luận (C) và \(\Delta\) có ít nhất 1 điểm chung \(\Rightarrow d\left(I;\Delta\right)\le R\) là đủ)
Đúng 1
Bình luận (2)