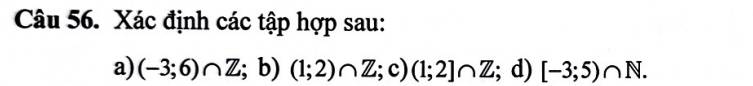mình đc gợi ý là giải bằng cách sơ đồ ven
Chương 1: MỆNH ĐỀ, TẬP HỢP
a: (-3;6) giao Z={-2;-1;0;1;2;3;4;5}
b: (1;2) giao Z=rỗng
c: \((1;2]\cap Z=\left\{2\right\}\)
d: \([-3;5)\cap N=\left\{0;1;2;3;4\right\}\)
Đúng 2
Bình luận (0)
Xác định tập hợp A ( -3;5] cup [8;10] cup [2;8)B [0;2] cup (-infty;5] cupleft(1;+inftyright)C [ -4;7] cup (0;10)D ( -infty;3 ] cupleft(-5;+inftyright)E left(3;+inftyright) ( -infty;1]F ( 1;3] [0;4)
Đọc tiếp
Xác định tập hợp
A = ( -3;5] \(\cup\) [8;10] \(\cup\) [2;8)
B = [0;2] \(\cup\) (\(-\infty;5\)] \(\cup\left(1;+\infty\right)\)
C = [ -4;7] \(\cup\) (0;10)
D = ( \(-\infty;3\) ] \(\cup\left(-5;+\infty\right)\)
E = \(\left(3;+\infty\right)\ \)\ ( \(-\infty;1\)]
F = ( 1;3] \ [0;4)
A=(-3;5] hợp [8;10] hợp [2;8)
=(-3;5) hợp [2;8) hợp [8;10]
=(-3;8) hợp [8;10]
=(-3;10]
B=[0;2] hợp (-vô cực;5] hợp (1;+vô cực)
=(-vô cực;5] hợp (1;+vô cực)
=(-vô cực;+vô cực)=R
C=[-4;7] hợp (0;10)
Vì (0;7] thuộc (0;10) nên [-4;7] hợp (0;10)=[-4;10)
D=(-vô cực;3] hợp (-5;+vô cực)
=(-5;3]
E=(3;+vô cực)\(-vô cực;1]
=(3;+vô cực)(Vì ko có phần tử nào có trong (3;+vô cực) nằm trong(-vô cực;1])
F=(1;3]\[0;4)=rỗng(Bởi vì (1;3] là tập con của [0;4))
Đúng 0
Bình luận (1)
Cho các đa thức f(x),�(�), g(x)�(�) và h(x).ℎ(�). Xét các tập hợp X{x∈R|f(x)0},�{�∈�|�(�)0}, Y{x∈R|g(x)0},�{�∈�|�(�)0}, Z{x∈R|h(x)0}�{�∈�|ℎ(�)0} và T{x∈R|f2(x)+|g(x)|+√h(x)≤0}.�{�∈�|�2(�)+|�(�)|+ℎ(�)≤0}. Trong các mệnh đề dưới đây, mệnh đề nào đúng ?A. TX∪Y∪Z.��∪�∪�.B. TX∩Y∩Z.��∩�∩�.C. TX
Đọc tiếp
Cho các đa thức và Xét các tập hợp và Trong các mệnh đề dưới đây, mệnh đề nào đúng ?
A.
B.
C.
Cho tam giác ABC vuông tại A, đường cao AH. Trên tia BC lấy điểm D sao
choBD BA . Đường vuông góc với BC tại D cắt AC tại E. Chứng minh rằng:
a) Điểm H nằm giữa B; D.
Page 15
b) BE là đường trung trực của đoạn AD.
c) Tia AD là tia phân giác của góc HAC.
d) HD DC
a: AH<AD
=>H nằm giữa B và D
b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
=>ΔBAE=ΔBDE
=>EA=ED
mà BA=BD
nên BE là trung trực của AD
c: góc CAD+góc BAD=90 độ
góc HAD+góc BDA=90 độ
mà góc BAD=góc BDA
nên góc CAD=góc HAD
=>AD là phân giác của góc HAC
Đúng 0
Bình luận (0)
 giúp mình câu 23 trở xuống với mình bí quá
giúp mình câu 23 trở xuống với mình bí quá
Cho tam giác ABC, có hai đường trung tuyến BM, CN. Chứng minh tam giác ANC = tam giác AMB. Chứng minh CN = BM
Sửa đề: ΔABC cân tại A
AB=AC
=>1/2AB=1/2AC
=>AN=AM
Xét ΔANC và ΔAMB có
AN=AM
góc NAC chung
AC=AB
=>ΔANC=ΔAMB
=>CN=BM
Đúng 0
Bình luận (0)
\(\sqrt{2x+4}-2\sqrt{2-x}=\dfrac{6x-4}{\sqrt{x^2+4}}\)
\(\Leftrightarrow\sqrt{2x+4}-\sqrt{8-4x}=\dfrac{6x-4}{\sqrt{x^2+4}}\)
\(\Leftrightarrow\dfrac{2x+4-8+4x}{\sqrt{2x+4}+\sqrt{8-4x}}=\dfrac{6x-4}{\sqrt{x^2+4}}\)
\(\Leftrightarrow\left(6x-4\right)\left(\dfrac{1}{\sqrt{2x+4}+\sqrt{8-4x}}-\dfrac{1}{\sqrt{x^2+4}}\right)=0\)
=>6x-4=0 hoặc \(\sqrt{x^2+4}=\sqrt{2x+4}+\sqrt{8-4x}\)
=>x=2/3 hoặc \(2x+4+8-4x+2\sqrt{\left(2x+4\right)\left(8-4x\right)}=x^2+4\)
=>x=2/3 hoặc \(x^2+4=-2x+12+2\sqrt{\left(2x+4\right)\left(8-4x\right)}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x^2+2x-8=2\sqrt{16x-4x^2+32-16x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\2\sqrt{-4x^2+32}=x^2+2x-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\4\sqrt{-x^2+16}=\left(x+4\right)\left(x-2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\\sqrt{-\left(x^2-16\right)}\cdot4-\sqrt{\left(x+4\right)^2\left(x-2\right)^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\16\left(-x^2+16\right)=\left(x+4\right)^2\cdot\left(x-2\right)^2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{2}{3}\\16\left(x-4\right)\left(x+4\right)+\left(x+4\right)^2\left(x-2\right)^2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\\left(x-4\right)\left(16x+64+\left(x^2-4x+4\right)\left(x+4\right)\right)=0\end{matrix}\right.\)
=>x=2/3 hoặc x=4
Đúng 1
Bình luận (0)
vecto BE+vecto BF-vecto DO
=1/2(vecto BA+vecto BC)-1/2 vecto DB
=1/2vecto BD-1/2vecto DB
=vecto BD
Đúng 0
Bình luận (0)