a) \(\dfrac{4}{x^2-2x+1}-\dfrac{6}{x^2-1}\)
Bài 6: Phép trừ các phân thức đại số
\(\dfrac{4}{x^2-2x+1}-\dfrac{6}{x^2-1}=\dfrac{4}{\left(x-1\right)^2}-\dfrac{6}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{\left(x-1\right)^2\left(x+1\right)}+\dfrac{-6.\left(x-1\right)}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{ 4+-6.\left(x+1\right)}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{-2.\left(x+1\right)}{\left(x-1\right)^2\left(x+1\right)}=-\dfrac{2}{\left(x-1\right)^2}\)
Đúng 1
Bình luận (1)
\(=\dfrac{4}{\left(x-1\right)^2}-\dfrac{6}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x+4-6x+6}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{10-2x}{\left(x-1\right)^2\left(x+1\right)}\)
Đúng 1
Bình luận (0)
Bài 1: Thực hiện phép chia:
a) \(\dfrac{5}{x}+\dfrac{x}{x+6}-\dfrac{30}{x^2+6x}\) với x ≠ -6 và x ≠ 0
b) \(\dfrac{3x+1}{\left(x-1\right)^2}-\dfrac{1}{x+1}+\dfrac{x+3}{1-x^2}\) với x ≠ \(\pm\)1
c) \(\dfrac{3x^2+2x+1}{x^3-1}-\dfrac{1-x}{x^2+x+1}-\dfrac{2}{x-1}\) với x ≠ 1
\(a,=\dfrac{5x+30+x^2-30}{x\left(x+6\right)}=\dfrac{x\left(x+5\right)}{x\left(x+6\right)}=\dfrac{x+5}{x+6}\\ b,=\dfrac{3x^2+4x+1-x^2+2x-1-x^2-2x+3}{\left(x-1\right)^2\left(x+1\right)}\\ =\dfrac{x^2+4x+3}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{x+3}{\left(x-1\right)^2}\)
\(c,=\dfrac{3x^2+2x+1+x^2-2x+1-2x^2-2x-2}{\left(x-1\right)\left(x^2+x+1\right)}\\ =\dfrac{2x^2-2x}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{2x}{x^2+x+1}\)
Đúng 1
Bình luận (0)
a) x+1/2x-6-4/2x-6 b) 3x-4/6x+3-x-5/6x+3
c) x-1/x-3-3x-8/3-x+3-2x/x-3 d) 3/x+5-5/x-7
e) 3/x+5-5/x-7 f) 2/x-2+3/x+2+5x-18/x2-4
Giúp mình với
Tìm Q:
1.\(\dfrac{2}{x^2-1}+Q=\dfrac{6}{x-3}-\dfrac{2x^2}{1-x^2}\)
giúp mik thực hiện phép trừ phân thức này với
a, \(\dfrac{1}{x^2-x+1}+1-\dfrac{x^2+2}{x^3+1}\)
\(=\dfrac{x+1}{x^3+1}+\dfrac{x^3+1}{x^3+1}-\dfrac{x^2+2}{x^3+1}\)
\(=\dfrac{x+1+x^3+1-x^2-2}{x^3+1}\)
\(=\dfrac{x^3-x^2+x}{x^3+1}=\dfrac{x\left(x^2-x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x}{x+1}\)
Đúng 1
Bình luận (0)
a,
= \(\dfrac{\left(4x+1\right).3}{2.3}-\dfrac{2\left(3x+2\right)}{2.3}\) = \(\dfrac{12x+3-6x-4}{6}=\dfrac{6x-1}{6}\)
Mình làm mẫu câu a cho bạn, mấy câu còn lại bạn tự làm nhé!
Bạn xem trong sách Toán 8 - Tập 1 có các bước để bạn giải, đơn giản lắm nha bạn ![]()
Đúng 0
Bình luận (0)
\(a,=\dfrac{12x+3-6x-4}{6}=\dfrac{6x-1}{6}\\ b,=\dfrac{x^2-9-x^2+9}{x\left(x-3\right)}=0\\ c,=\dfrac{3x}{5\left(x+y\right)}-\dfrac{x}{16\left(x-y\right)}=\dfrac{48x^2-48xy-5x^2-5xy}{80\left(x-y\right)\left(x+y\right)}\\ =\dfrac{43x^2-53xy}{80\left(x-y\right)\left(x+y\right)}\\ d,=\dfrac{5x^2-y^2-3x+2xy}{xy}\\ e,=\dfrac{x^4+2x^2+1-x^4-1}{x^2+1}=\dfrac{2x^2}{x^2+1}\\ f,=\dfrac{\left(3x+2\right)\left(x+1\right)^2-6\left(x^2-1\right)-\left(3x-2\right)\left(x-1\right)^2}{\left(x-1\right)^2\left(x+1\right)^2}\\ =\dfrac{10x^2+10}{\left(x-1\right)^2\left(x+1\right)^2}\)
Đúng 0
Bình luận (0)
Giúp e với ah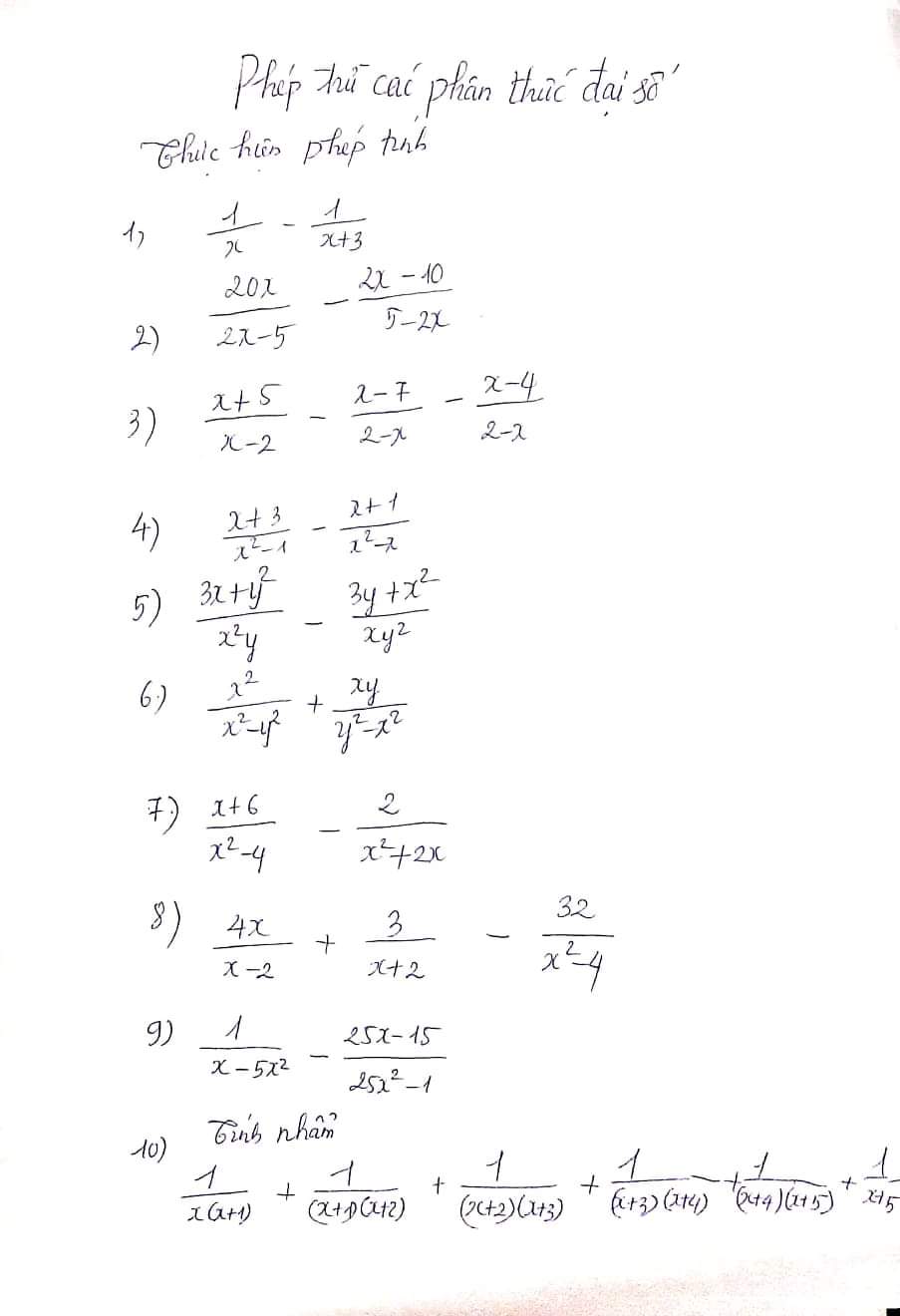
\(1,=\dfrac{x+3-x}{x\left(x+3\right)}=\dfrac{3}{x\left(x+3\right)}\\ 2,=\dfrac{20x+2x-10}{2x-5}=\dfrac{22x-10}{2x-5}\\ 3,=\dfrac{x+5+x-7+x-4}{x-2}=\dfrac{3\left(x-2\right)}{x-2}=3\\ 4,=\dfrac{x^2+3x-x^2-2x-1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{x\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x\left(x+1\right)}\\ 5,=\dfrac{3xy+y^3-3xy-x^3}{x^2y^2}=\dfrac{y^3-x^3}{x^2y^2}\\ 6,=\dfrac{x^2-xy}{\left(x-y\right)\left(x+y\right)}=\dfrac{x\left(x-y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{x}{x+y}\)
\(7,=\dfrac{x^2+6x-2x+4}{x\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)^2}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x+2}{x\left(x-2\right)}\\ 8,=\dfrac{4x^2+8x+3x-6-32}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x^2+11x-38}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-2\right)\left(4x+19\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x+19}{x+2}\\ 9,=\dfrac{-5x-1-25x^2+15x}{x\left(5x-1\right)\left(5x+1\right)}=\dfrac{-\left(5x-1\right)^2}{x\left(5x-1\right)\left(5x+1\right)}=\dfrac{1-5x}{x\left(5x+1\right)}\\ 10,=\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+...+\dfrac{1}{x-4}-\dfrac{1}{x+5}+\dfrac{1}{x+5}=\dfrac{1}{x}\)
Đúng 1
Bình luận (1)
Giúp mình vs an, mk đang cần gấp ạ. Xin đừng làm tất ạ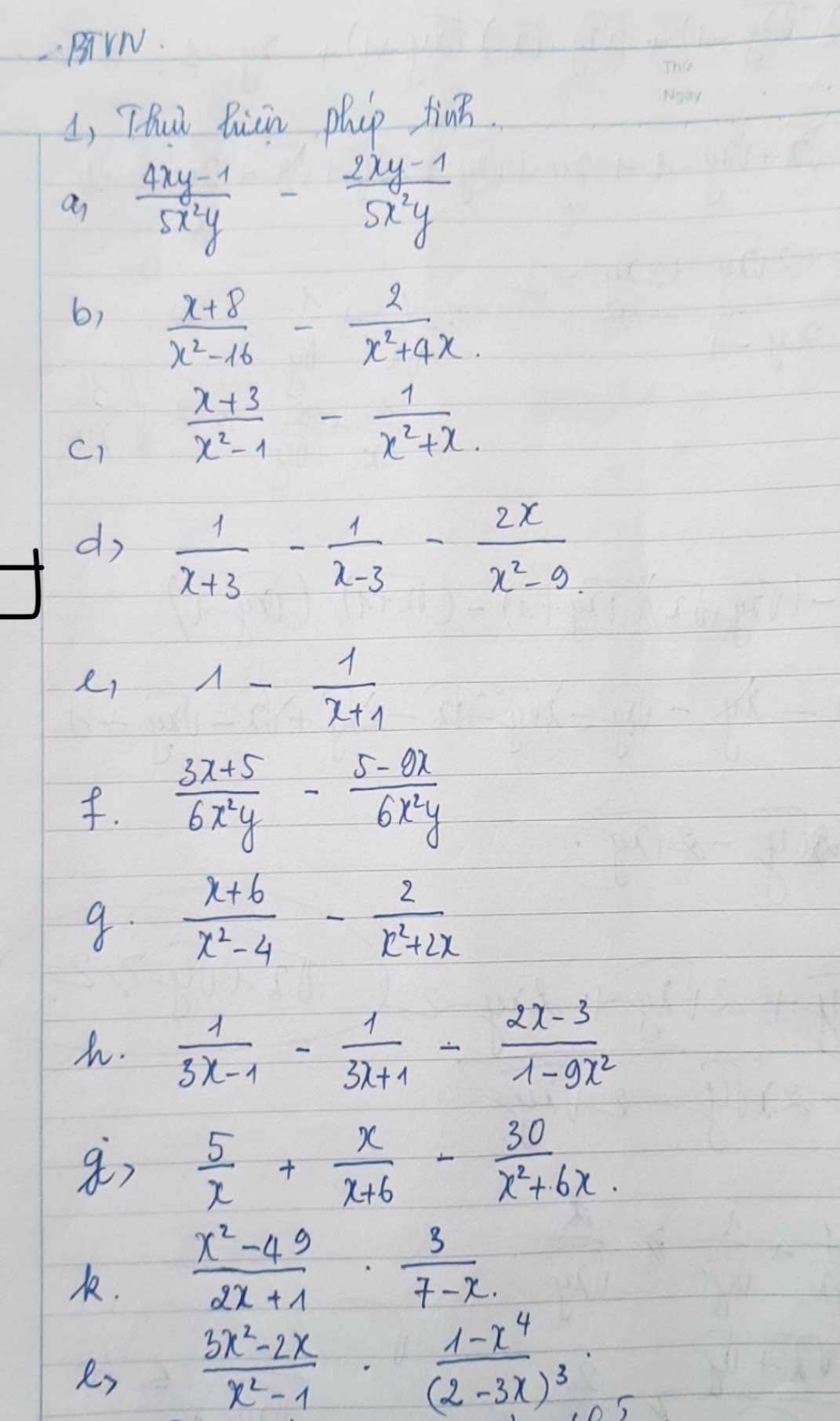
\(a,=\dfrac{4xy-1-2xy+1}{5x^2y}=\dfrac{6xy}{5x^2y}=\dfrac{6}{5x}\\ b,=\dfrac{x^2+8x-2x+8}{x\left(x-4\right)\left(x+4\right)}=\dfrac{\left(x+2\right)\left(x+4\right)}{x\left(x-4\right)\left(x+4\right)}=\dfrac{x+2}{x\left(x-4\right)}\\ c,=\dfrac{x^2+3x-x+1}{x\left(x+1\right)\left(x-1\right)}=\dfrac{\left(x+1\right)^2}{x\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{x\left(x-1\right)}\\ d,=\dfrac{x-3-x-3-2x}{\left(x-3\right)\left(x+3\right)}=\dfrac{-2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{3-x}\\ e,=\dfrac{x+1-1}{x+1}=\dfrac{x}{x+1}\\ f,=\dfrac{3x+5-5+9x}{6x^2y}=\dfrac{12x}{6xy}=\dfrac{2}{y}\)
Đúng 0
Bình luận (0)
\(g,=\dfrac{x^2+6x-2x+4}{x\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)^2}{x\left(x+2\right)\left(x-2\right)}=\dfrac{x+2}{x\left(x-2\right)}\\ h,=\dfrac{3x+1-3x+1+2x-3}{\left(3x-1\right)\left(3x+1\right)}=\dfrac{2x-1}{\left(3x-1\right)\left(3x+1\right)}\\ j,=\dfrac{5x+30+x^2-30}{x\left(x+6\right)}=\dfrac{x^2+5x}{x^2+6x}\\ k,=\dfrac{\left(x-7\right)\left(x+7\right)}{2x+1}\cdot\dfrac{-3}{x-7}=\dfrac{-3\left(x+7\right)}{2x+1}\\ l,=\dfrac{x\left(3x-2\right)}{x^2-1}\cdot\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{\left(3x-2\right)^3}=\dfrac{x\left(x^2+1\right)}{\left(3x-2\right)^2}\)
Đúng 0
Bình luận (0)
\(a,=\dfrac{3x-2-7x+4}{2xy}=\dfrac{-2\left(2x-1\right)}{2xy}=\dfrac{1-2x}{xy}\\ b,=\dfrac{3x+5-5+15x}{4x^3y}=\dfrac{18x}{4x^3y}=\dfrac{9}{2x^2y}\\ c,=\dfrac{4x+7-3x-6}{2x+2}=\dfrac{x+1}{2\left(x+1\right)}=\dfrac{1}{2}\\ d,=\dfrac{9x+5-5x+7}{2\left(x-1\right)\left(x+3\right)^2}=\dfrac{4\left(x+3\right)}{2\left(x-1\right)\left(x+3\right)^2}=\dfrac{2}{\left(x-1\right)\left(x+3\right)}\\ e,=\dfrac{xy+x^2}{\left(x-y\right)\left(x+y\right)}=\dfrac{x\left(x+y\right)}{\left(x-y\right)\left(x+y\right)}=\dfrac{x}{x-y}\)
\(f,=\dfrac{5xy+y^3-5xy+x^3}{x^2y^2}=\dfrac{x^3+y^3}{x^2y^2}\\ g,=\dfrac{2x^2-2x-x^2-x}{10\left(x+1\right)\left(x-1\right)}=\dfrac{x^2-3x}{10\left(x-1\right)\left(x+1\right)}\\ h,=\dfrac{x^2+9x-3x+9}{x\left(x-3\right)\left(x+3\right)}=\dfrac{\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}=\dfrac{x+3}{x\left(x-3\right)}\)
Đúng 2
Bình luận (0)
\(i,=\dfrac{3x-x+6}{2x\left(x+3\right)}=\dfrac{2\left(x+3\right)}{2x\left(x+3\right)}=\dfrac{1}{x}\\ j,=\dfrac{x^4-1-x^4+3x^2-2}{x^2-1}=\dfrac{3\left(x^2-1\right)}{x^2-1}=3\\ k,=\dfrac{x^2+4x+3+x^2-4x+3+2x-2x^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{2}{x-3}\\ l,=\dfrac{3x^2+4x+1-x^2+2x-1-x^2-2x+3}{\left(x-1\right)^2\left(x+1\right)}\\ =\dfrac{x^2+4x+3}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+3\right)}{\left(x-1\right)^2\left(x+1\right)}=\dfrac{x+3}{\left(x-1\right)^2}\)
\(n,=\dfrac{5x-15+6x^3-8x-6x^3+54x}{2x\left(x+3\right)\left(x-3\right)}=\dfrac{51x-15}{2x\left(x-3\right)\left(x+3\right)}\\ m,=\dfrac{\left(3x+1\right)\left(x+1\right)^2-6\left(x^2-1\right)-\left(3x-2\right)\left(x-1\right)^2}{\left(x-1\right)^2\left(x+1\right)^2}\\ =\dfrac{9x^2-2x+9}{\left(x-1\right)^2\left(x+1\right)^2}\)
Đúng 2
Bình luận (0)
\(\dfrac{2x^3+5}{x^2-x+1}-\dfrac{x^3+4}{x^2-x+1}\)help me :(
= \(\dfrac{2x^3+5-x^3-4}{x^2-x+1}\) = \(\dfrac{x^3-1}{x^2-x+1}\)
Đúng 0
Bình luận (0)
\(\dfrac{2x^3+5 -x^3-4}{x^2-x+1}=\dfrac{x^3+1 }{x+1}\)
Đúng 1
Bình luận (1)
câu này luôn \(\dfrac{2x^2y^5}{xy^2z}-\dfrac{4x^2y^3}{xy^2z}\)
Đúng 0
Bình luận (0)






