
Bài 4: Ôn tập chương Giới hạn
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{16+ax}-4}{4x}=\lim\limits_{x\rightarrow0}\dfrac{ax}{4x\left(\sqrt{16+ax}+4\right)}=\lim\limits_{x\rightarrow0}\dfrac{a}{4\left(\sqrt{16+ax}+4\right)}=\dfrac{a}{64}\)
\(\dfrac{a}{64}=2\Rightarrow a=128\)
Đúng 0
Bình luận (0)
cho hàm số f(x) thoả mãn \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-2}{x-3}=\dfrac{1}{4}\)
tính \(I=\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-2}{\left(x-3\right)\left(\sqrt{5f\left(x\right)+6}+1\right)}\)
Giúp em với ạ em cảm ơn nhìu!!!!!
Do \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-2}{x-3}\) hữu hạn \(\Rightarrow f\left(x\right)-2=0\) có nghiệm \(x=3\)
Hay \(f\left(3\right)-2=0\Rightarrow f\left(3\right)=2\)
\(\Rightarrow I=\lim\limits_{x\rightarrow3}\left(\dfrac{f\left(x\right)-2}{x-3}\right).\dfrac{1}{\sqrt{5f\left(x\right)+6}+1}=\dfrac{1}{4}.\dfrac{1}{\sqrt{5.f\left(3\right)+6}+1}\)
\(=\dfrac{1}{4}.\dfrac{1}{\sqrt{5.2+6}+1}=\dfrac{1}{20}\)
Đúng 1
Bình luận (1)
\(\lim\limits_{x\rightarrow\infty}\dfrac{1+Sin2x-Cos2x}{1-Sin2x-Cos2x}\)
Tính giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{1-Cosx.Cos2x}{x^2}\)
Ko sử dụng L'Hopital:
\(\lim\limits_{x\rightarrow0}\dfrac{1-cosx+cosx\left(1-cos2x\right)}{x^2}=\lim\limits_{x\rightarrow0}\dfrac{2sin^2\dfrac{x}{2}+2cosx.sin^2x}{x^2}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{1}{2}\left(\dfrac{sin\dfrac{x}{2}}{\dfrac{x}{2}}\right)^2+\lim\limits_{x\rightarrow0}2cosx\left(\dfrac{sinx}{x}\right)^2=\dfrac{1}{2}.1^2+2.1.1^2=\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
Tính giới hạn:
\(_{\lim\limits_{x\rightarrow\dfrac{\Pi}{4}}}\dfrac{\sqrt{2}Cosx-1}{\sqrt{2}Sinx-1}\)
Đặt \(t=x-\dfrac{\pi}{4}\), khi đó:
\(\lim\limits_{x\rightarrow\dfrac{\pi}{4}}\dfrac{\sqrt{2}cosx-1}{\sqrt{2}sinx-1}=\lim\limits_{t\rightarrow0}\dfrac{\sqrt{2}cos\left(t+\dfrac{\pi}{4}\right)-1}{\sqrt{2}sin\left(t+\dfrac{\pi}{4}\right)-1}\)
\(=\lim\limits_{t\rightarrow0}\dfrac{cost-sint-1}{cost+sint-1}\)
\(=\lim\limits_{t\rightarrow0}\dfrac{1-2sin^2\dfrac{t}{2}-2sin\dfrac{t}{2}.cos\dfrac{t}{2}-1}{1-2sin^2\dfrac{t}{2}+2sin\dfrac{t}{2}.cos\dfrac{t}{2}-1}\)
\(=\lim\limits_{t\rightarrow0}\dfrac{-2sin\dfrac{t}{2}\left(sin\dfrac{t}{2}+cos\dfrac{t}{2}\right)}{-2sin\dfrac{t}{2}\left(sin\dfrac{t}{2}-cos\dfrac{t}{2}\right)}\)
\(=\lim\limits_{t\rightarrow0}\dfrac{sin\dfrac{t}{2}+cos\dfrac{t}{2}}{sin\dfrac{t}{2}-cos\dfrac{t}{2}}\)
\(=-1\)
Đúng 1
Bình luận (0)
lim đề bài cho = \(\lim\limits_{x->\dfrac{\pi}{4}}\dfrac{-\sqrt{2}sinx}{\sqrt{2}cosx}\)
Thay x vào là xong
Đúng 0
Bình luận (1)
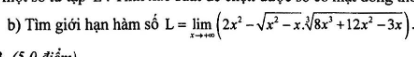
giúp em bài này với em cảm ơn ạ
\(L=\lim\limits_{x\rightarrow+\infty}\left(2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\right)\)
Đặt \(f\left(x\right)=2x^2-\sqrt{x^2-x}.\sqrt[3]{8x^3+12x^2-3x}\)
Ta có:
\(2.f\left(x\right)=4x^2-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(4x^2-1\right)-\sqrt{4x^2-4x}.\sqrt[3]{8x^3+12x^2-3x}\)
\(=1+\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)+\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
Đặt \(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(A\left(x\right)=\left(2x-1\right)\left(2x+1-\sqrt[3]{8x^3+12x^2-3x}\right)\)
\(=\dfrac{\left(2x-1\right)\left(8x^3+12x^2+6x+1-8x^3-12x^2+3x\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(=\dfrac{\left(2x-1\right)\left(9x+1\right)}{\left(2x+1\right)^2+\sqrt[3]{\left(8x^3+12x^2-3x\right)^2}+\left(2x+1\right)\sqrt[3]{8x^3+12x^2-3x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}A\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2-\dfrac{1}{x}\right)\left(9+\dfrac{1}{x}\right)}{\left(2+\dfrac{1}{x}\right)^2+\sqrt[3]{\left(8+\dfrac{12}{x}-\dfrac{3}{x^2}\right)^2}+\left(2+\dfrac{1}{x}\right)\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}\)
\(=\dfrac{2.9}{2^2+4+2.2}\)
\(=\dfrac{3}{2}\)
\(B\left(x\right)=\left(2x-1-\sqrt{4x^2-4x}\right).\sqrt[3]{8x^3+12x^2-3x}\)
\(=\dfrac{\left(4x^2-4x+1-4x^2+4x\right).\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(=\dfrac{\sqrt[3]{8x^3+12x^2-3x}}{2x-1+\sqrt{4x^2-4x}}\)
\(\Rightarrow\lim\limits_{x\rightarrow+\infty}B\left(x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{8+\dfrac{12}{x}-\dfrac{3}{x^2}}}{2-\dfrac{1}{x}+\sqrt{4-\dfrac{4}{x}}}\)
\(=\dfrac{2}{2+2}\)
\(=\dfrac{1}{2}\)
\(\Rightarrow2L=\lim\limits_{x\rightarrow+\infty}\left[2f\left(x\right)\right]\)
\(=\lim\limits_{x\rightarrow+\infty}\left[1+A\left(x\right)+B\left(x\right)\right]\)
\(=1+\lim\limits_{x\rightarrow+\infty}A\left(x\right)+\lim\limits_{x\rightarrow+\infty}B\left(x\right)\)
\(=1+\dfrac{3}{2}+\dfrac{1}{2}\)
\(=3\)
\(\Rightarrow L=\dfrac{3}{2}\)
Đúng 2
Bình luận (12)
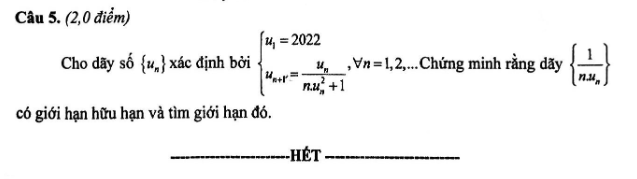 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ
\(\dfrac{1}{u_{n+1}}=\dfrac{1}{u_n}+nu_n\)
Đặt \(v_n=\dfrac{1}{u_n}\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{1}{2022}\\v_{n+1}=v_n+\dfrac{n}{v_n}\end{matrix}\right.\) và \(\left\{\dfrac{1}{nu_n}\right\}=\left\{\dfrac{v_n}{n}\right\}\)
Ta sẽ chứng minh \(v_n\ge n\) với \(n>1\)
Với \(n=2\Rightarrow v_2=v_1+2022>2\) (đúng)
Giả sử điều đó đúng với \(n=k>1\) hay \(v_k\ge k\)
Ta cần chứng minh \(v_{k+1}\ge k+1\)
Thật vậy, do \(v_k\ge k\), đặt \(v_k=k+\alpha\) với \(\alpha\ge0\)
Khi đó: \(v_{k+1}=v_k+\dfrac{k}{v_k}=k+\alpha+\dfrac{k}{k+\alpha}=k+\dfrac{k\alpha+\alpha^2+k}{k+\alpha}\ge k+\dfrac{\alpha+k}{k+\alpha}=k+1\) (đpcm)
Tương tự, ta quy nạp chứng minh được \(v_n\le n+v_2\) với \(n>1\) (do \(v_2\) số xấu nên ko ghi)
Kiểm tra với \(n=2\Rightarrow v_2\le2+v_2\) (đúng)
Giả sử \(v_k\le k+v_2\)
\(\Rightarrow v_{k+1}=v_k+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{v_k}\le k+v_2+\dfrac{k}{k}=k+1+v_2\) (đpcm)
\(\Rightarrow n\le v_n\le n+v_2\) \(\Rightarrow1\le\dfrac{v_n}{n}\le\dfrac{n+v_2}{n}\)
Sử dụng định lý kẹp, dễ dàng suy ra \(\lim\left\{\dfrac{v_n}{n}\right\}=1\)
Đúng 1
Bình luận (0)
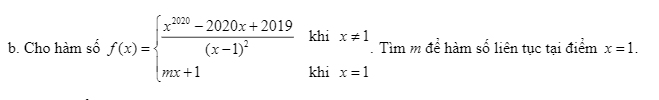
giúp em với em cảm ơn nhiềuuuu
Bài này xài L'Hopital đi, chứ tách biểu thức chắc đến sáng mai :D
\(\lim\limits_{x\rightarrow1}\dfrac{x^{2020}-2020x+2019}{\left(x-1\right)^2}=\lim\limits_{x\rightarrow1}\dfrac{2020x^{2019}-2020}{2\left(x-1\right)}=\lim\limits_{x\rightarrow1}\dfrac{2019.2020.x^{2018}}{2}=1010.2019\)
Hàm liên tục tại \(x=1\) khi: \(m+1=1010.2019\Rightarrow m=1010.2019-1\)
Đúng 2
Bình luận (0)

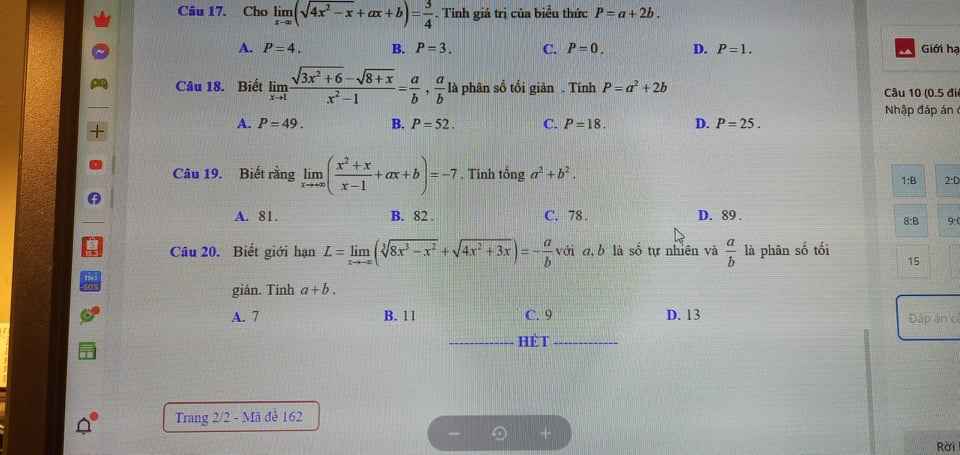
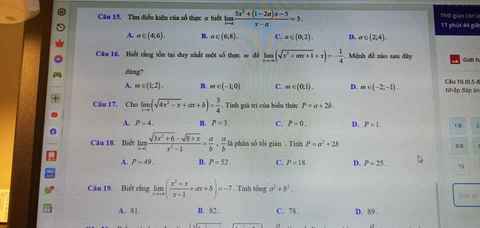
Giúp mình với ạ!
11.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{5x+\sqrt{3x^2-2}}{\sqrt{9x^2+1}-\left|x\right|}=\lim\limits_{x\rightarrow-\infty}\dfrac{5x+\left|x\right|\sqrt{3-\dfrac{2}{x^2}}}{\left|x\right|\sqrt{9+\dfrac{1}{x^2}}-\left|x\right|}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{5x-x\sqrt{3-\dfrac{2}{x^2}}}{-x\sqrt{9+\dfrac{1}{x^2}}+x}=\lim\limits_{x\rightarrow-\infty}\dfrac{5-\sqrt{3-\dfrac{2}{x^2}}}{-\sqrt{9+\dfrac{1}{x^2}}+1}\)
\(=\dfrac{5-\sqrt{3}}{-\sqrt{9}+1}=\dfrac{\sqrt{3}-5}{2}\)
\(\Rightarrow bc=-5.2=-10\)
Đúng 0
Bình luận (0)
12.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax^2-4x+5}{3x^2+3x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2\left(a-\dfrac{4}{x}+\dfrac{5}{x^2}\right)}{x^2\left(3+\dfrac{3}{x}+\dfrac{1}{x^2}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{a-\dfrac{4}{x}+\dfrac{5}{x^2}}{3+\dfrac{3}{x}+\dfrac{1}{x^2}}=\dfrac{a}{3}\)
\(\Rightarrow\dfrac{a}{3}=-2\Rightarrow a=-6\)
Đúng 0
Bình luận (0)
13.
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{5x^2+2x}-x\sqrt{5}+2\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{\left(\sqrt{5x^2+2x}-x\sqrt{5}\right)\left(\sqrt{5x^2+2x}+x\sqrt{5}\right)}{\sqrt{5x^2+2x}+x\sqrt{5}}+2\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{2x}{\sqrt{5x^2+2x}+x\sqrt{5}}+2\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{2}{\sqrt{5+\dfrac{2}{x}}+\sqrt{5}}+2\right)\)
\(=\dfrac{2}{2\sqrt{5}}+2=\dfrac{1}{5}.\sqrt{5}+2\)
\(\Rightarrow5a+b=5.\dfrac{1}{5}+2=3\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho f(x) = 1^4 +2^4+.....+n^4. Tìm f(x) bậc 5 sao cho f(x+1) - f(x) = x^4


