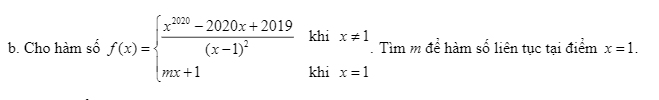11.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{5x+\sqrt{3x^2-2}}{\sqrt{9x^2+1}-\left|x\right|}=\lim\limits_{x\rightarrow-\infty}\dfrac{5x+\left|x\right|\sqrt{3-\dfrac{2}{x^2}}}{\left|x\right|\sqrt{9+\dfrac{1}{x^2}}-\left|x\right|}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{5x-x\sqrt{3-\dfrac{2}{x^2}}}{-x\sqrt{9+\dfrac{1}{x^2}}+x}=\lim\limits_{x\rightarrow-\infty}\dfrac{5-\sqrt{3-\dfrac{2}{x^2}}}{-\sqrt{9+\dfrac{1}{x^2}}+1}\)
\(=\dfrac{5-\sqrt{3}}{-\sqrt{9}+1}=\dfrac{\sqrt{3}-5}{2}\)
\(\Rightarrow bc=-5.2=-10\)
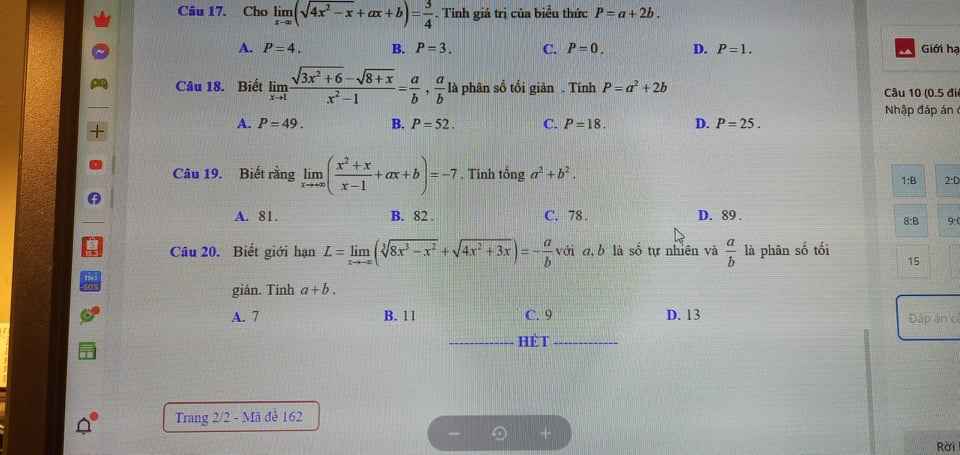
12.
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax^2-4x+5}{3x^2+3x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{x^2\left(a-\dfrac{4}{x}+\dfrac{5}{x^2}\right)}{x^2\left(3+\dfrac{3}{x}+\dfrac{1}{x^2}\right)}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{a-\dfrac{4}{x}+\dfrac{5}{x^2}}{3+\dfrac{3}{x}+\dfrac{1}{x^2}}=\dfrac{a}{3}\)
\(\Rightarrow\dfrac{a}{3}=-2\Rightarrow a=-6\)
13.
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{5x^2+2x}-x\sqrt{5}+2\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{\left(\sqrt{5x^2+2x}-x\sqrt{5}\right)\left(\sqrt{5x^2+2x}+x\sqrt{5}\right)}{\sqrt{5x^2+2x}+x\sqrt{5}}+2\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{2x}{\sqrt{5x^2+2x}+x\sqrt{5}}+2\right)\)
\(=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{2}{\sqrt{5+\dfrac{2}{x}}+\sqrt{5}}+2\right)\)
\(=\dfrac{2}{2\sqrt{5}}+2=\dfrac{1}{5}.\sqrt{5}+2\)
\(\Rightarrow5a+b=5.\dfrac{1}{5}+2=3\)
14.
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(5x-1\right)=5.2-1=9\)
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\left(x^2+1\right)=2^2+1=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\)
\(\Rightarrow\) Không tồn tại \(\lim\limits_{x\rightarrow2}f\left(x\right)\)
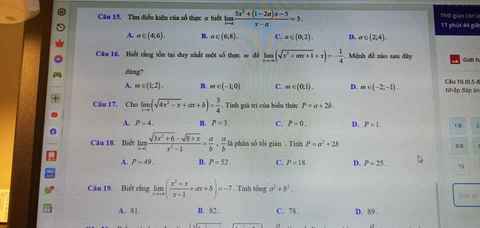
15.
Ko thấy rõ đề, là \(x\rightarrow a\) hay \(x\rightarrow2\) vậy nhỉ?
16.
\(\lim\limits_{x\rightarrow-\infty}\left(\sqrt{x^2+mx+1}+x\right)=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(\sqrt{x^2+mx+1}+x\right)\left(\sqrt{x^2+mx+1}-x\right)}{\sqrt{x^2+mx+1}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{mx+1}{\sqrt{x^2+mx+1}-x}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{m+\dfrac{1}{x}}{-\sqrt{1+\dfrac{m}{x}+\dfrac{1}{x^2}}-1}=-\dfrac{m}{2}\)
\(\Rightarrow-\dfrac{m}{2}=-\dfrac{1}{4}\Rightarrow m=\dfrac{1}{2}\)
17. Không thấy rõ đề, là \(x\rightarrow+\infty\) hay \(x\rightarrow-\infty\)
18.
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{3x^2+6}-\sqrt{8+x}}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3x^2+6-\left(8+x\right)}{\left(x-1\right)\left(x+1\right)\left(\sqrt{3x^2+6}+\sqrt{8+x}\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(3x+2\right)}{\left(x-1\right)\left(x+1\right)\left(\sqrt{3x^2+6}+\sqrt{8+x}\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{3x+2}{\left(x+1\right)\left(\sqrt{3x^2+6}+\sqrt{8+x}\right)}\)
\(=\dfrac{5}{2\left(3+3\right)}=\dfrac{5}{12}\)
19.
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{x^2+x}{x-1}+ax+b\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2+x+ax^2+bx-ax-b}{x-1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(a+1\right)x^2+\left(b-a+1\right)x-b}{x-1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(a+1\right)x+\left(b-a+1\right)-\dfrac{b}{x}}{1-\dfrac{1}{x}}\)
Giới hạn đã cho hữu hạn và bằng -7 khi:
\(\left\{{}\begin{matrix}a+1=0\\b-a+1=-7\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=-9\end{matrix}\right.\)
20.
\(=\lim\limits_{x\rightarrow-\infty}\left(\sqrt[3]{8x^3-x^2}-2x+\sqrt[]{4x^2+3x}+2x\right)\)
\(=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{-x^2}{\sqrt[3]{\left(8x^3-x^2\right)^2}+2x\sqrt[3]{8x^3-x^2}+4x^2}+\dfrac{3x}{\sqrt[]{4x^2+3x}-2x}\right)\)
\(=\lim\limits_{x\rightarrow-\infty}\left(\dfrac{-1}{\sqrt[3]{\left(8-\dfrac{1}{x}\right)^2}+2\sqrt[3]{8-\dfrac{1}{x}}+4}+\dfrac{3}{-\sqrt[]{4+\dfrac{3}{x}}-2}\right)\)
\(=\dfrac{-1}{4+4+4}+\dfrac{3}{-2-2}=-\dfrac{5}{6}\)



 giúp em với em cảm ơn nhiều ạ
giúp em với em cảm ơn nhiều ạ
 với ạ cần gấp ngày mai
với ạ cần gấp ngày mai