Bài 1: Khái niệm về mặt tròn xoay

I. SỰ TẠO THÀNH MẶT TRÒN XOAY

Trong không gian cho mặt phẳng \(\left(P\right)\) chứa đường thẳng \(\Delta\) và đường cong \(\left(C\right)\). Khi quay mặt phẳng \(\left(P\right)\) quanh \(\Delta\) một góc \(360^0\) thì đường cong \(\left(C\right)\) tạo nên một hình được gọi là mặt tròn xoay.

Đường cong \(\left(C\right)\) được gọi là đường sinh của mặt tròn xoay đó. Đường thẳng \(\Delta\) được gọi là trục của mặt tròn xoay.

II. MẶT NÓN TRÒN XOAY

1. Định nghĩa

Trong mặt phẳng \(\left(P\right)\), cho hai đường thẳng \(d\) và \(\Delta\) cắt nhau tại \(O\) và tạo thành góc \(\beta\left(0^o< \beta< 90^o\right)\). Khi quay mặt phẳng \(\left(P\right)\) xung quanh \(\Delta\) thì đường thẳng \(d\) sinh ra một mặt được gọi là mặt nón tròn xoay đỉnh \(O\) (hay mặt nón).

Đường thẳng \(\Delta\) là trục, đường thẳng \(d\) gọi là đường sinh và góc \(2\beta\) gọi là góc ở đỉnh của mặt nón đó.

2. Hình nón tròn xoay và khối nón tròn xoay

Cho tam giác \(OIM\) vuông tại \(I\). Khi quay tam giác đó quanh cạnh góc vuông \(OI\) thì đường gấp khúc \(OIM\) tạo thành một hình gọi là hình nón tròn xoay, gọi tắt là hình nón.

Hình tròn tâm \(I\) sinh bởi các điểm thuộc cạnh \(IM\) khi quay quanh trục \(OI\) được gọi là mặt đáy của hình nón, điểm \(O\) gọi là đỉnh của hình nón. Độ dài đoạn \(OI\) gọi là chiều cao của hình nón. Độ dài đoạn \(OM\) được gọi là độ dài đường sinh của hình nón. Phần mặt tròn xoay được sinh ra bởi các điểm trên cạnh \(OM\) khi quay quanh trục \(OI\) được gọi là mặt xung quanh của hình nón.

Khối nón tròn xoay (hay gọi tắt là khối nón) là phần không gian được giới hạn bởi một hình nón tròn xoay kể cả hình nón đó.

3. Diện tích xung quanh của khối nón tròn xoay

Diện tích xung quanh của hình nón tròn xoay bằng một nửa tích của độ dài đường tròn đáy và độ dài đường sinh. Tức là nếu bán kính đáy của hình nón là \(r\), độ dài đường sinh là \(l\) thì diện tích xung quanh của hình nón được tính theo công thức:

\(S_{xq}=\pi rl\)

Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy:

\(S_{tp}=S_{xq}+S_đ=\pi rl+\pi r^2\)

4. Thể tích khối nón tròn xoay

Thể tích \(V\) của khối nón tròn xoay có diện tích đáy \(B\) và chiều cao \(h\) là: 

\(V=\dfrac{1}{3}Bh\)

Như vậy nếu bán kính đáy bằng \(r\) thì \(B=\pi r^2\) nên \(V=\dfrac{1}{3}\pi r^2h\).

III. MẶT TRỤ TRÒN XOAY

1. Định nghĩa

Trong mặt phẳng \(\left(P\right)\) cho hai đường thẳng \(\Delta\) và \(l\) song song với nhau, cách nhau một khoảng bằng \(r\). Khi quay mặt phẳng \(\left(P\right)\) xung quanh \(\Delta\) thì đường thẳng \(l\) sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay (gọi tắt là mặt trụ). Đường thẳng \(\Delta\) gọi là trục, đường thẳng \(l\) là đường sinh và \(r\) là bán kính của mặt trụ đó.

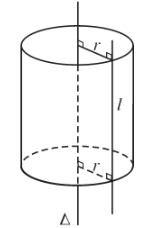
2. Hình trụ tròn xoay và khối trụ tròn xoay

Xét hình chữ nhật \(ABCD\). Khi quay hình đó quanh một đường thẳng chứa một cạnh, chẳng hạn cạnh \(AB\), thì đường gấp khúc \(ADCB\) tạo thành một hình được gọi là hình trụ tròn xoay hay còn được gọi tắt là hình trụ.

Khối trụ tròn xoay (hay khối trụ) là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó.

3. Diện tích xung quanh của hình trụ tròn xoay

Diện tích xung quanh của hình trụ tròn xoay bằng tích của chu vi đường tròn đáy và độ dài đường sinh.

Tức là nếu đáy của hình trụ tròn xoay là hình tròn bán kính \(r\), độ dài đường sinh là \(l\) thì diện tích xung quanh của hình trụ đó được tính theo công thức:

\(S_{xq}=2\pi rl\)

 Diện tích toàn phần của hình trụ bằng tổng diện tích xung quanh và diện tích đáy:

\(S_{tp}=S_{xq}+S_đ=2\pi rl+2\pi r^2\)

4. Thể tích khối trụ tròn xoay

Gọi \(V\) là thể tích của khối trụ tròn xoay có diện tích đáy \(B\) và chiều cao \(h\), ta có công thức:

\(V=Bh\)

Như vậy,  nếu bán kính đáy là \(r\) thì \(B=\pi r^2\), suy ra

 \(V=\pi R^2h.\)