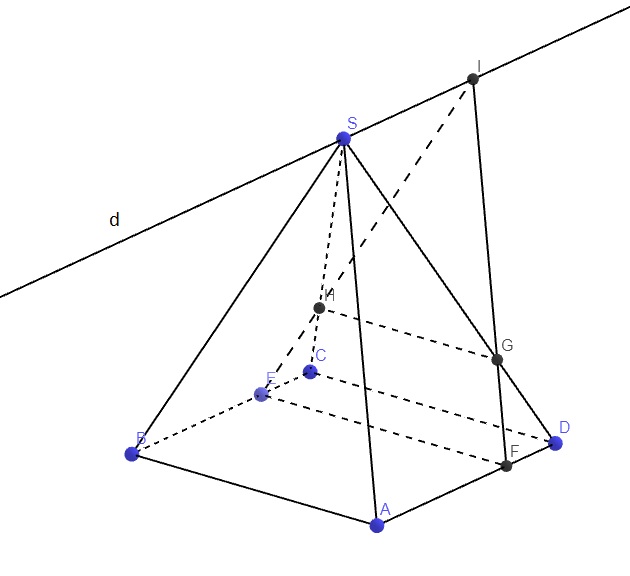
Bài 2: Hai đường chéo nhau và hai đường thẳng song song

a.

Ta có: \(\left\{{}\begin{matrix}EF||AB\\GH||CD\end{matrix}\right.\) mà \(AB||CD\)

\(\Rightarrow EF||GH\)

\(\Rightarrow4\) điểm E, F, G, H đồng phẳng

b.

Theo định lý Talet, do \(EH||SB\Rightarrow\dfrac{CE}{CB}=\dfrac{CH}{CS}\)

Mà ABCD là hbh và \(EF||AB\Rightarrow ABEF\) là hbh \(\Rightarrow BE=AF\Rightarrow\dfrac{CE}{CB}=\dfrac{DF}{DA}\)

\(\Rightarrow\dfrac{DF}{DA}=\dfrac{CH}{CS}\)

Do \(GH||CD\Rightarrow\dfrac{CH}{CS}=\dfrac{DG}{DS}\)

\(\Rightarrow\dfrac{DF}{DA}=\dfrac{DG}{DS}\Rightarrow GF||SA\) theo Talet đảo

c.

Qua S kẻ đường thẳng d song song AD và BC 

Mà \(S\in\left(SAD\right)\cap\left(SBC\right)\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)

Có \(\left\{{}\begin{matrix}EH\in\left(SBC\right)\\SG\in\left(SAD\right)\end{matrix}\right.\)  \(\Rightarrow EH\cap SG\in\left(SBC\right)\cap\left(SAD\right)\)

\(\Rightarrow I\in d\) cố định

Vậy khi E di động trên BC thì I chạy trên giao tuyến của (SAD) và (SBC)

Chọn D

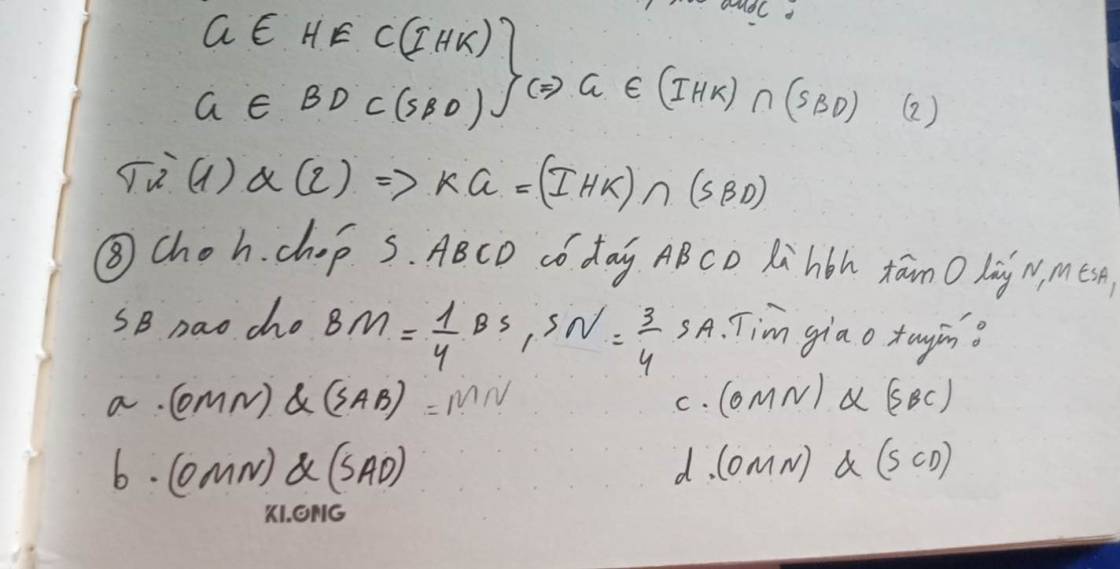
a: M thuộc SB 

N thuộc SA

=>(OMN) giao (SAB)=MN

b: Gọi giao của MO với SD là E

=>E thuộc (MNO) giao (SAD)

=>(MNO) giao (SAD)=EN

c: gọi giao của NO với AC là F

=>Fthuộc (MNO) giao (SBC)

=>(MNO) giao (SBC)=FM

32.

Gọi T là biến cố "Trong 10 người được chọn có ít nhất 2 người là nữ".

\(\Rightarrow\overline{T}\) là biến cố "Trong 10 người được chọn không có quá 1 người là nữ"

\(\Rightarrow\left|\Omega\right|=C^{10}_{20}\)

TH1: Trong 10 người được chọn chỉ có 1 người là nữ.

\(\Rightarrow\) Có \(C^9_{12}.C^1_8\) cách chọn.

TH2: Cả 10 người được chọn đều là nam.

\(\Rightarrow\) Có \(C^{10}_{12}\) cách chọn.

\(\Rightarrow\left|\Omega_{\overline{T}}\right|=C^9_{12}.C^1_8+C^{10}_{12}\)

\(\Rightarrow P\left(\overline{T}\right)=\dfrac{\left|\Omega_{\overline{T}}\right|}{\left|\Omega\right|}=\dfrac{C^9_{12}.C^1_8+C^{10}_{12}}{C^{10}_{20}}=\dfrac{83}{8396}\)

\(\Rightarrow P\left(T\right)=1-P\left(\overline{T}\right)=\dfrac{8315}{8396}\)