Bài 14: Số nguyên tố. Hợp số. Bảng số nguyên tố
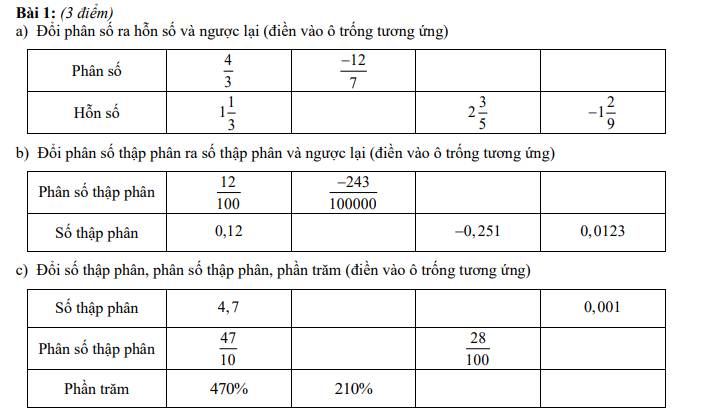
a:
| phân số | \(\dfrac{4}{3}\) | \(-\dfrac{12}{7}\) | \(\dfrac{13}{5}\) | \(-\dfrac{11}{9}\) |
| hỗn số | \(1\dfrac{1}{3}\) | \(-1\dfrac{5}{7}\) | \(2\dfrac{3}{5}\) | \(-1\dfrac{2}{9}\) |
b:
| Phân số thập phân | 12/100 | \(-\dfrac{243}{100000}\) | \(-\dfrac{251}{1000}\) | \(\dfrac{123}{10000}\) |
| Số thập phân | 0,12 | -0,00243 | -0,251 | 0,0123 |
c:
| Số thập phân | 4,7 | 2,1 | 0,28 | 0,001 |
| Phân số thập phân | \(\dfrac{47}{10}\) | \(\dfrac{21}{10}\) | \(\dfrac{28}{100}\) | \(\dfrac{1}{1000}\) |
| Phần trăm | 470% | 210% | 28% | 0,1% |
Đúng 1
Bình luận (0)
chứng minh 4n+3/8n+2 là phân số tối giản (với n thuộc N sao)
giả giúp mik với ạ
Gọi d=ƯCLN(4n+3;8n+2)
=>\(\left\{{}\begin{matrix}4n+3⋮d\\8n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8n+6⋮d\\8n+2⋮d\end{matrix}\right.\)
=>\(8n+6-8n-2⋮d\)
=>\(4⋮d\)
mà 4n+3 lẻ
nên d=1
=>ƯCLN(4n+3;8n+2)=1
=>\(\dfrac{4n+3}{8n+2}\) là phân số tối giản
Đúng 2
Bình luận (0)
Gọi \(d=ƯC\left(4n+3;8n+2\right)\) với \(d\in N\)*
\(\Rightarrow\left\{{}\begin{matrix}4n+3⋮d\\8n+2⋮d\end{matrix}\right.\)
\(\Rightarrow2\left(4n+3\right)-\left(8n+2\right)⋮d\)
\(\Rightarrow4⋮d\) \(\Rightarrow\left[{}\begin{matrix}d=1\\d=2\\d=4\end{matrix}\right.\)
Mặt khác do \(4n+3\) luôn lẻ, mà các số tự nhiên lẻ chỉ có các ước lẻ \(\Rightarrow d\) là số lẻ
\(\Rightarrow d=1\)
\(\Rightarrow4n+3\) và \(8n+2\) nguyên tố cùng nhau
\(\Rightarrow\dfrac{4n+3}{8n+2}\) là phân số tối giản
Đúng 1
Bình luận (0)
chứng minh rằng với n lẻ và n thuộc n* thì 7 n+ 24 không là số chính phương
Do n lẻ \(\Rightarrow n=2k+1\)
Đặt \(a=7^n+24=7^{2k+1}+24=7.49^k+24\)
Do \(\left\{{}\begin{matrix}49\equiv1\left(mod4\right)\\7\equiv3\left(mod4\right)\\24\equiv0\left(mod4\right)\end{matrix}\right.\) \(\Rightarrow7.49^k+24\equiv3\left(mod4\right)\)
Mà các số chính phương chia 4 chỉ có các số dư 0 hoặc 1
\(\Rightarrow a\) không thể là SCP hay \(7^n+24\) ko là SCP với mọi số tự nhiên lẻ n
Đúng 1
Bình luận (0)
tìm số nguyên n để :
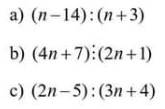
a: \(n-14⋮n+3\)
=>\(n+3-17⋮n+3\)
=>\(-17⋮n+3\)
=>\(n+3\in\left\{1;-1;17;-17\right\}\)
=>\(n\in\left\{-2;-4;14;-20\right\}\)
b: \(4n+7⋮2n+1\)
=>\(4n+2+5⋮2n+1\)
=>\(5⋮2n+1\)
=>\(2n+1\inƯ\left(5\right)\)
=>\(2n+1\in\left\{1;-1;5;-5\right\}\)
=>\(2n\in\left\{0;-2;4;-6\right\}\)
=>\(n\in\left\{0;-1;2;-3\right\}\)
c: \(2n-5⋮3n+4\)
=>\(6n-15⋮3n+4\)
=>\(6n+8-23⋮3n+4\)
=>\(-23⋮3n+4\)
=>\(3n+4\in\left\{1;-1;23;-23\right\}\)
=>\(3n\in\left\{-3;-5;19;-27\right\}\)
=>\(n\in\left\{-1;-\dfrac{5}{3};\dfrac{19}{3};-9\right\}\)
mà n nguyên
nên \(n\in\left\{-1;-9\right\}\)
Đúng 1
Bình luận (0)
tìm số nguyên x,y : 3x (y + 2) + y + 2 = 13
\(3x(y+2)+y+2=13\\\Rightarrow3x(y+2)+(y+2)=13\\\Rightarrow(y+2)(3x+1)=13\)
Vì \(x,y\) nguyên nên \(3x+1;y+2\) nguyên
\(\Rightarrow3x+1;y+2\) là các ước của \(13\)
Ta có bảng sau:
| \(3x+1\) | \(1\) | \(13\) | \(-1\) | \(-13\) |
| \(y+2\) | \(13\) | \(1\) | \(-13\) | \(-1\) |
| \(x\) | \(0\) | \(4\) | \(-\dfrac{2}{3}\) | \(-\dfrac{14}{3}\) |
| \(y\) | \(11\) | \(-1\) | \(-15\) | \(-3\) |
Mà \(x,y\) nguyên nên ta được: \(\left(x;y\right)=\left\{\left(0;11\right);\left(4;-1\right)\right\}\)
Đúng 3
Bình luận (0)
2x+7 chia hết cho 2x-2 với x là số nguyên. Help!!!
\(2x+7⋮2x-2\)
=>\(2x-2+9⋮2x-2\)
=>\(9⋮2x-2\)
=>\(2x-2\in\left\{1;-1;3;-3;9;-9\right\}\)
=>\(2x\in\left\{3;1;5;-1;11;-7\right\}\)
=>\(x\in\left\{\dfrac{3}{2};\dfrac{1}{2};\dfrac{5}{2};-\dfrac{1}{2};\dfrac{11}{2};-\dfrac{7}{2}\right\}\)
mà x nguyên
nên \(x\in\varnothing\)
Đúng 0
Bình luận (0)
2x-7 chia hết cho 2x-2 với x là số nguyên
2x-7\(⋮2x-2\)
=>\(2x-2-5⋮2x-2\)
=>\(-5⋮2x-2\)
=>\(2x-2\in\left\{1;-1;5;-5\right\}\)
=>\(2x\in\left\{3;1;7;-3\right\}\)
=>\(x\in\left\{\dfrac{3}{2};\dfrac{1}{2};\dfrac{7}{2};-\dfrac{3}{2}\right\}\)
mà x nguyên
nên \(x\in\varnothing\)
Đúng 0
Bình luận (0)
Tìm số nguyên tố p để:
p+2 , p+6 đều là số nguyên tố ![]()
Bạn xem lại đề đã viết đúng chưa vậy?
Đúng 0
Bình luận (0)
điền vào chỗ trống;
-5......>-25
-5>-25 là đúng rồi mà điền một số nx là sai mà
Đúng 0
Bình luận (0)
Cho p,q là các số nguyên tố lớn hơn 3 thoản mãn p – q = 2. Chứng minh p + q chia hết cho 12.
Vì q là số nguyên tố lớn hơn 3 nên q có dạng 3k+1 hoặc 3k+2. (\(k\in N\)*)
Nếu q=3k+1 thì p=q+2=3k+3. Khi đó p chia hết cho 3 nên không phải số nguyên tố (loại)
Nếu q=3k+2 thì p=q+2=3k+4. Khi đó p+q=6k+6=6(k+1)
Vì q=3k+2 là số nguyên tố nên k là số lẻ (nếu k chẵn thì q chia hết cho 2). Khi đó k có dạng 2m+1 (\(m\in N\)*)
Suy ra p+q=6(2m+1+1)=12(m+1) chia hết cho 12 (đpcm)
Đúng 0
Bình luận (0)




