Bài 11. Phương pháp giải một số bài toán về toàn mạch

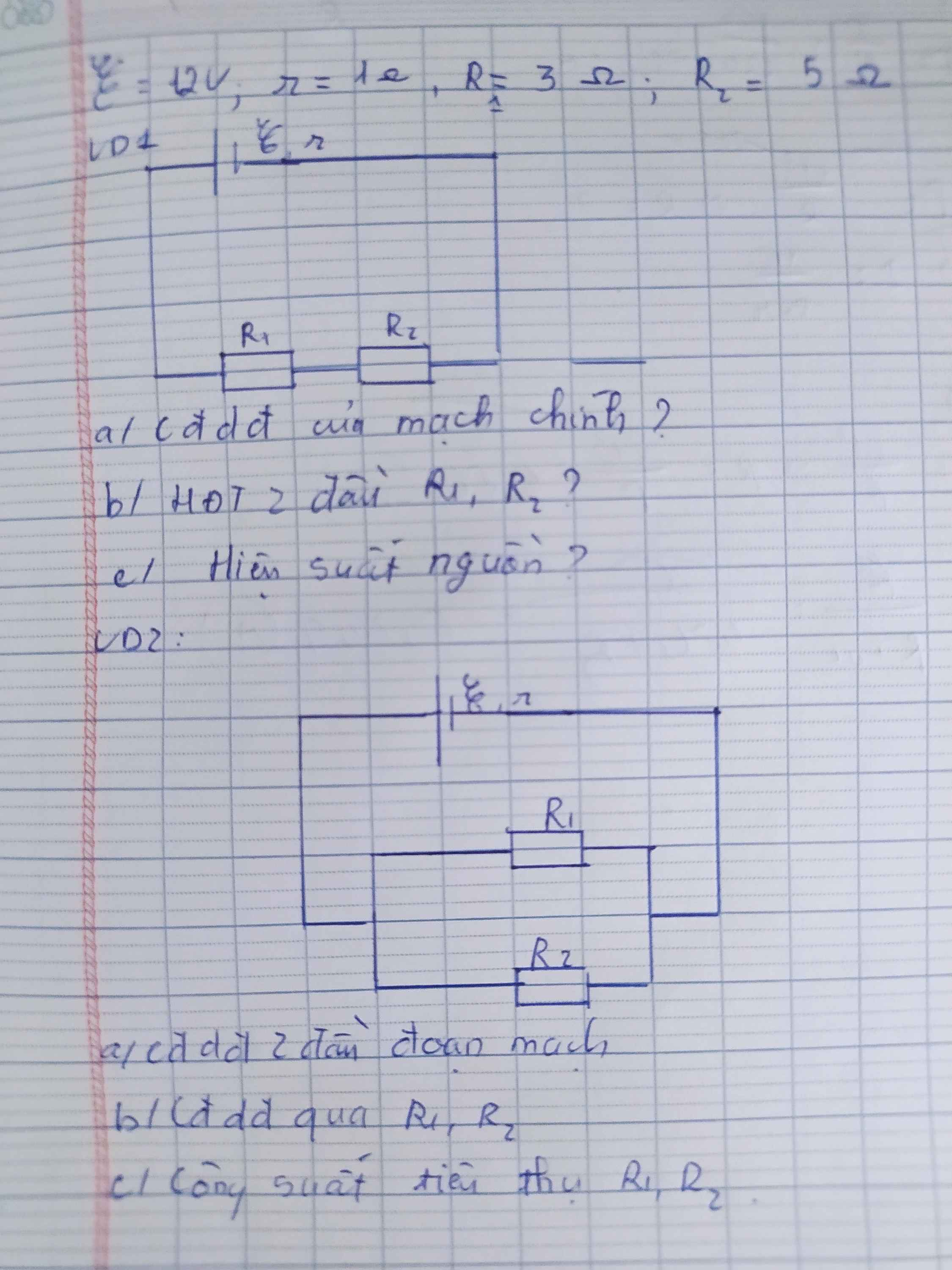
Ví dụ 1:

\(R_1ntR_2\Rightarrow R_N=R_1+R_2=3+5=8\Omega\)

a)\(I=\dfrac{\xi}{R_N+r}=\dfrac{12}{1+8}=\dfrac{4}{3}A\)

b)\(I_1=I_2=I=\dfrac{4}{3}A\)

\(U_1=I_1\cdot R_1=\dfrac{4}{3}\cdot3=4V;U_2=I_2R_2=\dfrac{4}{3}\cdot5=\dfrac{20}{3}V\)

c)\(U_N=U_1+U_2=4+\dfrac{20}{3}=\dfrac{32}{3}V\)

Hiệu suất nguồn: \(H=\dfrac{U_N}{\xi}\cdot100\%=\dfrac{\dfrac{32}{3}}{12}\cdot100\%=88,89\%\)

Ví dụ 2:

\(R_1//R_2\Rightarrow R_N=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{3\cdot5}{3+5}=\dfrac{15}{8}\Omega\)

a)\(I=\dfrac{\xi}{R_N+r}=\dfrac{12}{\dfrac{15}{8}+1}=\dfrac{96}{23}A\)

b)\(U_N=\xi-I\cdot r=12-\dfrac{96}{23}\cdot1=\dfrac{180}{23}V\)

\(R_1//R_2\Rightarrow U_1=U_2=U_N=\dfrac{180}{23}V\)

\(I_1=\dfrac{U_1}{R_1}=\dfrac{\dfrac{180}{23}}{3}=\dfrac{60}{23}A;I_2=\dfrac{U_2}{R_2}=\dfrac{\dfrac{180}{23}}{5}=\dfrac{36}{23}A\)

c)\(P_1=\dfrac{U_1^2}{R_1}=\dfrac{\left(\dfrac{180}{23}\right)^2}{3}\approx20,42W\)

\(P_2=\dfrac{U_2^2}{R_2}=\dfrac{\left(\dfrac{180}{23}\right)^2}{5}\approx12,25W\)

em ơi đề thiếu

\(\overrightarrow{E_{MA}}+\overrightarrow{E_{MB}}=\overrightarrow{0}\)

\(\Leftrightarrow\left\{{}\begin{matrix}E_{MA}=E_{MB}\\\overrightarrow{E_{MA}}\uparrow\downarrow\overrightarrow{E_{MB}}\end{matrix}\right.\Leftrightarrow9\cdot10^9\cdot\dfrac{3\cdot10^9}{MA^2}=9\cdot10^9\cdot\dfrac{\left|q_2\right|}{MB^2}\)

\(\Leftrightarrow\left|q_2\right|=1.2\cdot10^{12}\cdot MB^2\)

TH1: q1q2<0

=>M nằm ngoài đoạn AB

=>M sẽ nằm gần A hơn

=>MA+AB=MB

=>MB=5+10=15cm

=>q2=2,7*10^10(C)=27nC

TH2: q1q2>0

=>q2<0

=>M nằm giữa A và B

=>MB=5cm

=>|q2|=3*10^9

=>q2=-3*10^9(C)

a, \(\xi_b=\xi_1+\xi_2=7,5+7,5=15\left(V\right)\)

\(r_b=r_1+r_2=1+1=2\left(\Omega\right)\)

b,\(R=\dfrac{R_2\cdot\left(R_1+R_3\right)}{R_2+R_1+R_3}=\dfrac{40\cdot\left(40+20\right)}{40+40+20}=24\left(\Omega\right)\)

\(I=\dfrac{\xi_b}{R+r_b}=\dfrac{15}{24+2}=\dfrac{15}{26}\left(A\right)\)

c,\(U_{AB}=I\cdot R=\dfrac{15}{26}\cdot24=\dfrac{180}{13}\left(V\right)\)

\(I_{AD}=I_{DB}=I_{AB}=\dfrac{U_{AB}}{R_1+R_3}=\dfrac{\dfrac{180}{13}}{40+20}=\dfrac{3}{13}\left(A\right)\)

\(U_{AD}=R_1I_{AD}=40\cdot\dfrac{3}{13}=\dfrac{120}{13}\left(V\right)\)

\(U_{DB}=R_1I_{DB}=20\cdot\dfrac{3}{13}=\dfrac{60}{13}\left(V\right)\)

d,\(P_1=U_{AD}\cdot I_{AD}=\dfrac{120}{13}\cdot\dfrac{3}{13}=\dfrac{360}{169}\left(W\right)\)

\(P_2=\dfrac{U_{AB}^2}{R_2}=\dfrac{\left(\dfrac{180}{13}\right)^2}{40}=\dfrac{810}{169}\left(W\right)\)

\(P_3=U_{DB}\cdot I_{DB}=\dfrac{60}{13}\cdot\dfrac{3}{13}=\dfrac{180}{169}\left(W\right)\)

e,\(A_1=P_1t=\dfrac{360}{169}\cdot300\approx639,05\left(J\right)\)

\(P_b=I^2R=\left(\dfrac{15}{26}\right)^2\cdot24=\dfrac{1350}{169}\left(W\right)\)

\(MCD:R1nt\left(R2//R3\right)\)

\(\Rightarrow R=R1+\dfrac{R2\cdot R3}{R2+R3}=5+\dfrac{15\cdot10}{15+10}=11\Omega\)

\(\Rightarrow I=\dfrac{\xi}{R+r}=\dfrac{12}{11+1}=1A\)

\(I=I1=I23=1A\)

\(U=IR=1\cdot11=11A\)

\(\Rightarrow U1=I1\cdot R1=1\cdot5=5V\)

\(\Rightarrow U23=U2=U3=U-U1=11-5=6V\)

\(\Rightarrow\left\{{}\begin{matrix}I2=U2:R2=6:15=0,4A\\I3=U3:R3=6:10=0,6A\end{matrix}\right.\)