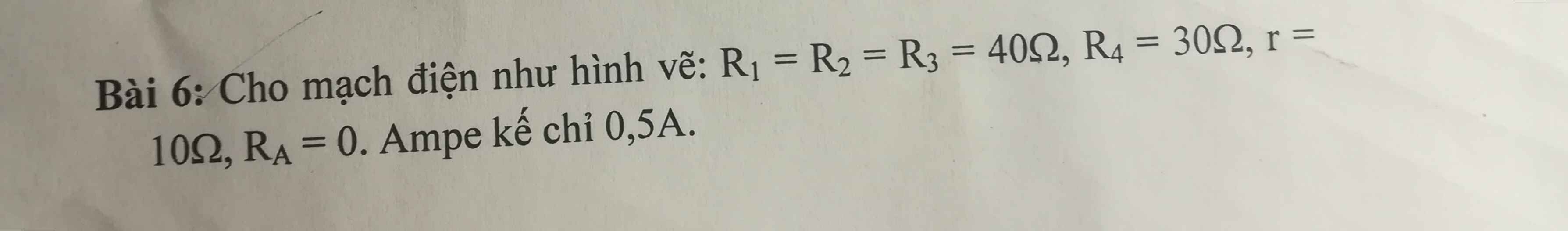Câu 2(3diem) : Cho đoạn mạch gồm hai bóng đèn loại 200V - 40V và 200V-60W mắc nối tiếp. a, Tìm điện năng tiêu thụ trên hai đèn trong thời gian 30 phút. b, Tỉnh điện trở của hai đến. c, tính điện trở tương đương của đoạn mạch.
Bài 11. Phương pháp giải một số bài toán về toàn mạch
\(30p=0,5h\)
a. \(\left\{{}\begin{matrix}A1=P1.t=40.0,5=20\left(Wh\right)=72000\left(J\right)\\A2=P2.t=60.0,5=30\left(Wh\right)=108000\left(J\right)\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}R1=\dfrac{U1^2}{P1}=\dfrac{200^2}{40}=1000\Omega\\R2=\dfrac{U2^2}{P2}=\dfrac{200^2}{60}=\dfrac{2000}{3}\Omega\end{matrix}\right.\)
c. \(R=R1+R2=1000+\dfrac{2000}{3}=\dfrac{5000}{3}\Omega\)
Đúng 0
Bình luận (0)
Cho mạch điện như hình vẽ, cho biết:R1 4 ôm; R2 R5 20ôm; R3 R6 12ôm; R4 R7 8ôm; UAB 48V.a) Tìm điện trở tương đương RAB của đoạn mạch.b) Tìm cường độ dòng điện và hiệu điện thế chạy qua các điện trở.
Đọc tiếp
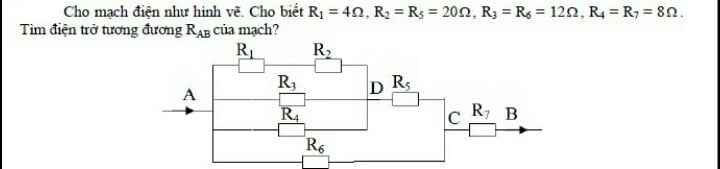
Cho mạch điện như hình vẽ, cho biết:
R1 = 4 ôm; R2 = R5 = 20ôm; R3 = R6 = 12ôm; R4 = R7 = 8ôm; UAB = 48V.
a) Tìm điện trở tương đương RAB của đoạn mạch.
b) Tìm cường độ dòng điện và hiệu điện thế chạy qua các điện trở.
a, \(=>\dfrac{1}{R1234}=\dfrac{1}{\left(R1+R2\right)}+\dfrac{1}{R3}+\dfrac{1}{R4}=>\dfrac{1}{R1234}=\dfrac{1}{24}+\dfrac{1}{12}+\dfrac{1}{8}=>R1234=4\left(om\right)\)
\(=>Rab=R7+\dfrac{R6\left(R5+R1234\right)}{R6+R5+R1234}=8+\dfrac{12\left(20+4\right)}{12+20+4}=16\left(om\right)\)
b.,\(=>I7=123456=\dfrac{U}{Rab}=\dfrac{48}{16}=3A=>U7=I7.R7=24V=>U123456=48-24=24V\)
\(=>U123456=U6=U12345=24V=>I6=\dfrac{U6}{R6}=2A=>I12345=\dfrac{24}{R12345}=\dfrac{24}{24}=1A=I5=I1234\)
\(=>U5=I5R5=20V,=>U1234=24-20=4V=U12=U3=U4\)
\(=>I3=\dfrac{U3}{R3}=\dfrac{4}{12}=\dfrac{1}{3}A,=>I4=\dfrac{U4}{R4}=\dfrac{4}{8}=0,5A\)
\(=I12=I1=I2=\dfrac{4}{24}=\dfrac{1}{6}A=>U1=I1R1=\dfrac{2}{3}V=>U2=I2R2=\dfrac{10}{3}V\)
(bài dài nên bn bấm lại máy tính ktra cho chắc)
Đúng 2
Bình luận (0)
2.Một vận động viên đẩy tạ, lúc ra tạ ở độ cao 1,56m với vận tốc ban đầu là 43,2km/h, góc ra tạ hợp với phương thẳng đứng là 600. Hỏi:
a. Tầm xa của quả tạ?
b. Độ cao lớn nhất mà tạ đạt được?
c. Tầm xa tại góc tọa độ của quả tạ?
d. Đường đi của quả tạ?
e. Tầm xa cực đai của quả tạ?
Cho mạch điện như hình vẽ nguồn điện có hiệu suất điện động 24V điện trở trong 4 ôm các điện trở ngoài R1 3 ôm R2 6 ôm và một bóng đèn 12 V 8w tính a tính cường độ dòng điện qua các điện trở và công suất của nguồn điện đèn có sáng bình thường không tính P thực tế của đèn thay đèn ở trên bằng một bình điện phân dung dịch AgNO3 với Anot bằng Ag có điện trở r điện phân 18 ôm tính khối lượng bạc bám vào catốt trong thời gian 20 phút 5 giây
Đọc tiếp
Cho mạch điện như hình vẽ nguồn điện có hiệu suất điện động 24V điện trở trong 4 ôm các điện trở ngoài R1 = 3 ôm R2 = 6 ôm và một bóng đèn 12 V 8w tính a tính cường độ dòng điện qua các điện trở và công suất của nguồn điện đèn có sáng bình thường không tính P thực tế của đèn thay đèn ở trên bằng một bình điện phân dung dịch AgNO3 với Anot bằng Ag có điện trở r điện phân = 18 ôm tính khối lượng bạc bám vào catốt trong thời gian 20 phút 5 giây
Cho em hỏi: Nguồn điện có sđđ6,6V và điện trở trong r0,12(ôm). Bóng đèn đ1 loại 6V-3W; bóng đèn 2 loại 2,5V-1,25W. Các đèn sáng bình thường. Tính: a) Hiệu điện thế 2 đầu mỗi bóng đèn. b) Hiệu điện thế 2 đầu điện trở R2, cường độ dòng điện qua R2 và giá trị của R2. c) Cường độ dòng điện trong mạch và hiệu điện thế giữa 2 điểm AB?
d) Hiệu điện thế giữa 2 đầu R1 và giá trị của R1. e) Với giá trị nào của R2 thì công suất tiêu thụ ở mạch ngoài là lớn nhất. f) Với giá trị nào của R2 để công suất trên...
Đọc tiếp
Cho em hỏi: Nguồn điện có sđđ=6,6V và điện trở trong r=0,12(ôm). Bóng đèn đ1 loại 6V-3W; bóng đèn 2 loại 2,5V-1,25W. Các đèn sáng bình thường. Tính: a) Hiệu điện thế 2 đầu mỗi bóng đèn. b) Hiệu điện thế 2 đầu điện trở R2, cường độ dòng điện qua R2 và giá trị của R2. c) Cường độ dòng điện trong mạch và hiệu điện thế giữa 2 điểm AB?
d) Hiệu điện thế giữa 2 đầu R1 và giá trị của R1. e) Với giá trị nào của R2 thì công suất tiêu thụ ở mạch ngoài là lớn nhất. f) Với giá trị nào của R2 để công suất trên R2 lớn nhất
Một động cơ điện có hiệu suất 90% làm việc bình thường ở U=100V có thể nâng đều vật nặng 50kg lên cao 160cm trong 10s. Cho g=10m/s^2.Tính cường độ dòng điện chạy qua động cơ
Xem chi tiết
Công có ích cần để nâng vật là: \(A_i=P.h=mgh=50.10.1,6=800\left(J\right)\)
=> Công toàn phần là: \(A_{tp}=\dfrac{A_i}{H}=\dfrac{800}{0,9}=\dfrac{8000}{9}\left(J\right)\)
\(\Rightarrow P_{tp}=\dfrac{A_{tp}}{t}=\dfrac{8000}{9.10}=\dfrac{800}{9}\left(W\right)\Rightarrow I=\dfrac{P}{U}=\dfrac{800}{9.100}=\dfrac{8}{9}\left(A\right)\)
Đúng 2
Bình luận (0)
 Cho một mạch điện như hình vẽ suất điện động 12,5 V ,r =0,5 Ω,R1 =10 Ω,R2 =25Ω ,đèn có ghi 5,5 V - 4W. a, Tính cường độ dòng điện qua mạch b, Đèn sáng như thế nào ? vì sao ? c, Tính công suất và hiệu điện suát của nguồn
Cho một mạch điện như hình vẽ suất điện động 12,5 V ,r =0,5 Ω,R1 =10 Ω,R2 =25Ω ,đèn có ghi 5,5 V - 4W. a, Tính cường độ dòng điện qua mạch b, Đèn sáng như thế nào ? vì sao ? c, Tính công suất và hiệu điện suát của nguồn
a/\(R_D=\dfrac{U^2}{P}=\dfrac{5,5^2}{4}=\dfrac{121}{16}\left(\Omega\right)\)
\(\Rightarrow R_{mach-ngoai}=\dfrac{\left(R_1+R_D\right).R_2}{R_1+R_D+R_2}=...\left(\Omega\right)\)
\(I=\dfrac{\xi}{R_{mach-ngoai}+r}=\dfrac{12,5}{0,5+R_{mach-ngoai}}=...\left(A\right)\)
b/ \(U_{mach-ngoai}=U_{1D}=U_2=I.R_{mach-ngoai}=...\left(V\right)\)
\(\Rightarrow I_D=I_1=\dfrac{U_{1D}}{R_D+R_1}=...\left(A\right)\)
\(I_{Den-dinh-muc}=\dfrac{P}{U}=\dfrac{4}{5,5}=\dfrac{8}{11}\left(A\right)\)
\(\left[{}\begin{matrix}I_D>I_{Den-dinh-muc}\Rightarrow den-sang-yeu-hon-binh-thuong\\I_D< I_{Den-dinh-muc}\Rightarrow den-sang-manh-hon-binh-thuong\\I_D=I_{Den-dinh-muc}\Rightarrow den-sang-binh-thuong\end{matrix}\right.\)
Đúng 1
Bình luận (1)
trong mạch gồm các điên trở R1=3 r2=5 mắc vào 1 hiệu điện thế u =12v dúng ampe kế đo được i=1,5a hói hai điện trở mắc theo kiểu nào... mọi người giúp em với mai em nộp r ạ
R1 nối tiếp R2. Muốn thử thì vận dụng địng luật Ôm, I = U/(R1+R2)
Đúng 0
Bình luận (0)
Một nguồn điện có suất điện động 150V và điện trở trong 2 ôm. Dùng nguồn điện này để thắp sáng bình thường các bóng đèn có giá trị định mức 120V-180W. Số bóng đèn được thắp sáng tối đa là bao nhiêu?
Bài làm:
Cường độ qua đèn khi sáng bình thường là:
I0 = \(\dfrac{P_đ}{U_đ}\) = \(\dfrac{180}{120}\) = 1,5A
Điện trở của đèn là:
R0 = \(\dfrac{P_đ^2}{U_đ}\) = \(\dfrac{180^2}{120}\) = 270Ω
Giả sử các đèn mắc thành y dãy song song, mỗi dãy có x đèn nối tiếp
⇒Cường độ dòng điện mạch chính là:
I = y.I0
Theo định luật Ôm cho mạch kín:
I = \(\dfrac{E}{R+r}\)
⇔ y.I0 = \(\dfrac{E}{\dfrac{xR_0}{y}+r}\)
⇒ xR0I0 + yI0.r = E
⇔ 120x + 180y = 150
⇔ 4x + 6y = 5 (1)
Dùng bất đẳng thức Cô-si, ta có:
4x + 6y ≥ \(\sqrt{5xy}\)
Số đèn tổng cộng là: N = xy
⇒ \(\sqrt{5N}\) ≤ 5
hay N ≤ 5
⇒ Số đèn tối đa có thể thắp sáng bình thường là: N = 5.
Vậy số đèn có thể lắp tối đa là 5 bóng đèn.
Đúng 0
Bình luận (3)