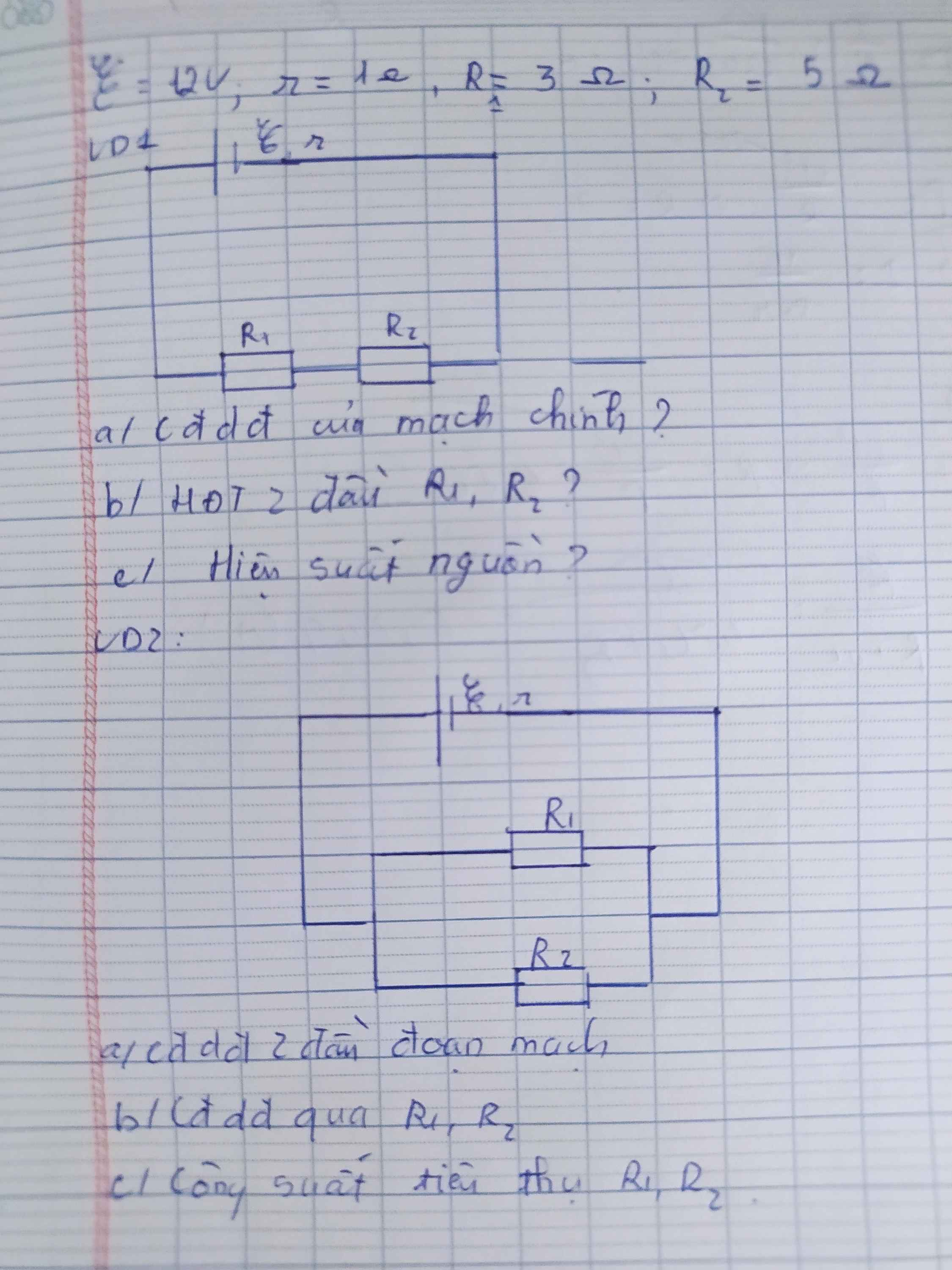
Ví dụ 1:
\(R_1ntR_2\Rightarrow R_N=R_1+R_2=3+5=8\Omega\)
a)\(I=\dfrac{\xi}{R_N+r}=\dfrac{12}{1+8}=\dfrac{4}{3}A\)
b)\(I_1=I_2=I=\dfrac{4}{3}A\)
\(U_1=I_1\cdot R_1=\dfrac{4}{3}\cdot3=4V;U_2=I_2R_2=\dfrac{4}{3}\cdot5=\dfrac{20}{3}V\)
c)\(U_N=U_1+U_2=4+\dfrac{20}{3}=\dfrac{32}{3}V\)
Hiệu suất nguồn: \(H=\dfrac{U_N}{\xi}\cdot100\%=\dfrac{\dfrac{32}{3}}{12}\cdot100\%=88,89\%\)
Ví dụ 2:
\(R_1//R_2\Rightarrow R_N=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{3\cdot5}{3+5}=\dfrac{15}{8}\Omega\)
a)\(I=\dfrac{\xi}{R_N+r}=\dfrac{12}{\dfrac{15}{8}+1}=\dfrac{96}{23}A\)
b)\(U_N=\xi-I\cdot r=12-\dfrac{96}{23}\cdot1=\dfrac{180}{23}V\)
\(R_1//R_2\Rightarrow U_1=U_2=U_N=\dfrac{180}{23}V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{\dfrac{180}{23}}{3}=\dfrac{60}{23}A;I_2=\dfrac{U_2}{R_2}=\dfrac{\dfrac{180}{23}}{5}=\dfrac{36}{23}A\)
c)\(P_1=\dfrac{U_1^2}{R_1}=\dfrac{\left(\dfrac{180}{23}\right)^2}{3}\approx20,42W\)
\(P_2=\dfrac{U_2^2}{R_2}=\dfrac{\left(\dfrac{180}{23}\right)^2}{5}\approx12,25W\)