Tìm tập xác định của các hàm số :
a. \(y=\dfrac{3x-2}{2x+1}\)
b. \(y=\dfrac{x-1}{x^2+2x-3}\)
c. \(y=\sqrt{2x+1}-\sqrt{3-x}\)
Cho hàm số :
\(y=\left\{{}\begin{matrix}x+1;\left(x\ge2\right)\\x^2-2;\left(x< 2\right)\end{matrix}\right.\)
Tính giá trị của hàm số đó tại \(x=3;x=-1;x=2\) ?
Với x ≥ 2 hàm số có công thức y= f(x) = x + 1.
Vậy giá trị của hàm số tại x = 3 là f(3) = 3 + 1 = 4.
Tương tự, với x < 2 hàm số có công thức y = f(y) = x2 - 2.
Vậy f(- 1) = (- 1)2 – 2 = - 1.
Tại x = 2 giá trị của hàm số là: f(2) = 2 + 1 = 3.
Trả lời: f(3) = 4; f(- 1) = - 1; f(2) = 3.
Trả lời bởi Hiiiii~
Cho hàm số \(y=3x^2-2x+1\)
Các điểm sau đó thuộc đồ thị của hàm số đó không ?
a. \(M\left(-1;6\right)\)
b. \(N\left(1;1\right)\)
c. \(P\left(0;1\right)\)
a) Điểm A(x0;y0) thuộc đồ thị (G) của hàm số y = f(x) có tập xác định D khi và chỉ khi: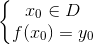 
Tập xác định của hàm số y = 3x2 – 2x + 1 là D = R.
Ta có : -1 ∈ R, f(- 1) = 3(- 1)2 – 2(- 1) + 1 = 6
Vậy điểm M(- 1;6) thuộc đồ thị hàm số đã cho.
b) Ta có: 1 ∈ R, f(1) = 3 (1)2 – 2(1) + 1 = 2 ≠ 1.
Vậy N(1;1) không thuộc đồ thị đã cho.
c) P(0;1) thuộc đồ thị đã cho.
Trả lời bởi Hiiiii~
Xét tính chẵn lẻ của các hàm số :
a. \(y=\left|x\right|\)
b. \(y=\left(x+2\right)^2\)
c. \(y=x^3+x\)
d. \(y=x^2+x+1\)
a) Tập xác định của y = f(x) = |x| là D = R.
∀x ∈ R => -x ∈ R
f(- x) = |- x| = |x| = f(x)
Vậy hàm số y = |x| là hàm số chẵn.
b) Tập xác định của
y = f(x) = (x + 2)2 là R.
x ∈ R => -x ∈ R
f(- x) = (- x + 2)2 = x2 – 4x + 4 ≠ f(x)
f(- x) ≠ - f(x) = - x2 – 4x - 4
Vậy hàm số y = (x + 2)2 không chẵn, không lẻ.
c) D = R, x ∈ D => -x ∈ D
f(– x) = (– x3) + (– x) = - (x3 + x) = – f(x)
Vậy hàm số đã cho là hàm số lẻ.
d) Hàm số không chẵn cũng không lẻ.
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi \(y=f\left(x\right),y=g\left(x\right),y=h\left(x\right)\) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lại vào thời gian x. Qua biểu đồ, hãy :
a) Tìm tập xác của mỗi hàm số đã nêu ?
b) Tìm các giá trị \(f\left(2002\right);g\left(1999\right);h\left(2000\right)\) và nêu ý nghĩa của chúng ?
c) Tính hiệu \(h\left(2002\right)-h\left(1999\right)\) và nêu ý nghĩa của nó ?
a) Txđ: D =\(\left[1998;+\infty\right]\)
b) \(f\left(2002\right)=620000\) con.
\(g\left(1999\right)=380000\) con.
\(h\left(2000\right)=100000\) con.
c) \(h\left(1999\right)=30000\) con; \(h\left(2002\right)=210000\).
\(h\left(2002\right)-h\left(1999\right)=210000-30000=180000\).
Ý nghĩa: Hiệu \(h\left(2002\right)-h\left(1999\right)\) thể hiện sự tăng trưởng sản lượng ngan qua giai đoạn 1999 - 2002.
Tìm tập xác định của các hàm số ?
a) \(y=-x^5+7x-3\)
b) \(y=\dfrac{3x+2}{x-4}\)
c) \(y=\sqrt{4x+1}-\sqrt{-2x+1}\)
d) \(y=\dfrac{\sqrt{x+9}}{x^2+8x-20}\)
e) \(y=\dfrac{2x+1}{\left(2x+1\right)\left(x-3\right)}\)
f) \(y=\dfrac{7+x}{x^2+2x-5}\)
a) TXĐ: \(D=R\).
b) \(TXD=D=R\backslash\left\{4\right\}\)
c) Đkxđ: \(\left\{{}\begin{matrix}4x+1\ge0\\-2x+1\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{-1}{4}\\x\le\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{-1}{4}\le x\le\dfrac{1}{2}\).
TXĐ: D = \(\left[\dfrac{-1}{4};\dfrac{1}{2}\right]\)
Cho hàm số :
\(y=f\left(x\right)=\left\{{}\begin{matrix}\dfrac{2x-3}{x-1};\left(x\le0\right)\\-x^2+2x;\left(x>0\right)\end{matrix}\right.\)
Tính giá trị của hàm số đó tại \(x=5;x=-2;x=0;x=2\) ?
\(f\left(5\right)=-5^2+2.5=-15\)
\(f\left(-2\right)=-\left(-2\right)^2+2.\left(-2\right)=-8\)
\(f\left(2\right)=-2^2+2.2=0\)
Cho các hàm số \(f\left(x\right)=x^2+2+\sqrt{2-x};g\left(x\right)=-2x^3-3x+5\)
\(u\left(x\right)=\left\{{}\begin{matrix}\sqrt{3-x};\left(x< 2\right)\\\sqrt{x^2-4};\left(x\ge2\right)\end{matrix}\right.\)
\(v\left(x\right)=\left\{{}\begin{matrix}\sqrt{6-x};\left(x\le0\right)\\x^2+1;\left(x>0\right)\end{matrix}\right.\)
Tính các giá trị \(f\left(-2\right)-f\left(1\right);f\left(-7\right)-g\left(-7\right);f\left(-1\right)-u\left(-1\right);u\left(3\right)-v\left(3;\right)v\left(0\right)-g\left(0\right);\dfrac{f\left(2\right)-f\left(-2\right)}{v\left(2\right)-v\left(-3\right)}\) ?
\(f\left(-2\right)-f\left(1\right)=\left(-2\right)^2+2+\sqrt{2-\left(-2\right)}-\left(1^2+2+\sqrt{2-1}\right)\) \(=8-4=4\).
\(f\left(-7\right)-g\left(-7\right)=\left(-7\right)^2+2+\sqrt{2-\left(-7\right)}-\left(-2.\left(-7\right)^3-3.\left(-7\right)+5\right)=-658\)
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng ?
a) \(y=-2x+3\) trên R
b) \(y=x^2+10x+9\) trên \(\left(-5;+\infty\right)\)
c) \(y=-\dfrac{1}{x+1}\) trên \(\left(-3;-2\right)\) và \(\left(2;3\right)\)
a) hệ số a=-2=>y luôn nghịch biến
b) a=1 >0 và -b/2a =-5 => (-5;+vc) y luôn đồng biến
c) hàm y có dạng y=a/(x+1)
a =-1 => y đồng biến (-vc;-1) nghich biến (-1;+vc
=>
(-3;-2) hàm y đồng biến
(2;3) hàm y đồng biến
Trả lời bởi ngonhuminhXét tính chẵn, lẽ của các hàm số :
a) \(y=-2\)
b) \(y=3x^2-1\)
c) \(y=-x^4+3x-2\)
d) \(y=\dfrac{-x^4+x^2+1}{x}\)
lời giải
a) Hàm chẵn
b) f(x) =f(-x)=>hàm chẵn
c) không chẵn, không lẻ
d)f(-x) =\(\dfrac{-x^4+x^2+1}{-x}=-\dfrac{-x^4+x^2+1}{x}=-f\left(x\right)\) =>hàm lẻ
Trả lời bởi ngonhuminh
a) Công thức
có nghĩa với x ∈ R sao cho 2x + 1 ≠ 0.
Vậy tập xác định của hàm số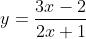
là:
D = { x ∈ R/2x + 1 ≠ 0} =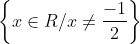
b) Tương tự như câu a), tập xác định của hàm số đã cho là:
D = { x ∈ R/x2 + 2x - 3 ≠ 0}
x2 + 2x – 3 = 0 ⇔ x = -3 hoặc x = 1
Vậy D = R {- 3; 1}.
c)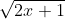
có nghĩa với x ∈ R sao cho 2x + 1 ≥ 0
Vậy tập xác định của hàm số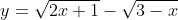
là:
D = D1 ∩ D2, trong đó:
D1 = {x ∈ R/2x + 1 ≥ 0} =
D2 = {x ∈ R/3 - x ≥ 0} =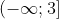
Trả lời bởi Hiiiii~