§1. Cung và góc lượng giác

I. KHÁI NIỆM CUNG VÀ GÓC LƯỢNG GIÁC

1. Đường tròn định hướng và cung lượng giác

- Khái niệm:

Đường tròn định hướng là một đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ làm chiều dương. 

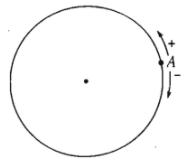
Trên đường tròn định hướng cho hai điểm \(A\) và \(B\). Một điểm \(M\) di động trên đường tròn luôn theo một chiều (âm hoặc dương) từ \(A\) đến \(B\) tạo nên một cung lượng giác có điểm đầu \(A\) điểm cuối \(B\).

Với hai điểm \(A\), \(B\) đã cho trên đường tròn định hướng ta có vô số cung lượng giác có điểm đầu \(A\), điểm cuối \(B\). Mỗi cung như vậy đều được kí hiệu là 

Ví dụ:

+) Nếu điểm \(M\) di động theo chiều ngược với chiều quay của kim đồng hồ từ điểm đầu \(A\) và dừng lại ngay tại \(B\) khi gặp \(B\) lần đầu, ta được một cung lượng giác như sau:

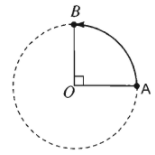
+) Nếu điểm \(M\) di động theo chiều ngược với chiều quay của kim đồng hồ từ điểm đầu \(A\) và dừng lại tại \(B\) sau khi quay thêm một vòng rồi gặp \(B\) lần thứ hai, ta được một cung lượng giác như sau:

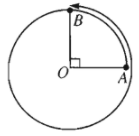
+) Nếu điểm \(M\) di động theo chiều cùng chiều với chiều quay của kim đồng hồ từ điểm đầu \(A\) và dừng lại ngay tại điểm cuối \(B\) khi gặp \(B\) lần đầu, ta được một cung lượng giác như sau:

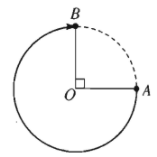
- Chú ý: Trên một đường tròn định hướng, lấy hai điểm \(A\) và \(B\)

     Kí hiệu \(\stackrel\frown{AB}\) chỉ một cung hình học (cung lớn hoặc cung bé) hoàn toàn xác định.

     Kí hiệu  chỉ một cung lượng giác điểm đầu \(A\), điểm cuối \(B\).

2. Góc lượng giác