Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau :
a) \(y=x^{\sqrt{3}}\)
b) \(y=x^{\dfrac{1}{\pi}}\)
c) \(y=x^{-e}\)
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau :
a) \(y=x^{\sqrt{3}}\)
b) \(y=x^{\dfrac{1}{\pi}}\)
c) \(y=x^{-e}\)
Tìm tập xác định của các hàm số sau :
a) \(y=\dfrac{2}{\sqrt{4^x-2}}\)
b) \(y=\log_6\dfrac{3x+2}{1-x}\)
c) \(y=\sqrt{\log x+\log\left(x+2\right)}\)
d) \(y=\sqrt{\log\left(x-1\right)+\log\left(x+1\right)}\)
Biết \(4^x+4^{-x}=23\) . Hãy tính \(2^x+2^{-x}\)
Giải các bất phương trình :
a) \(2^{2x-1}+2^{2x-2}+2^{2x-3}\ge448\)
b) \(\left(0,4\right)^x-\left(2,5\right)^{x+1}>1,5\)
c) \(\log_3\left[\log_{\dfrac{1}{2}}\left(x^2-1\right)\right]< 1\)
d) \(\log^2_{0,2}x-5\log_{0,2}x< -6\)
Cho \(\log_ab=3;\log_ac=-2\). Hãy tính \(\log_ax\) với :
a) \(x=a^3b^2\sqrt{c}\)
b) \(x=\dfrac{a^4\sqrt[3]{b}}{c^3}\)
Tìm tập xác định của các hàm số :
a) \(y=\dfrac{1}{3^x-3}\)
b) \(y=\log\dfrac{x-1}{2x-3}\)
c) \(y=\log\sqrt{x^2-x-12}\)
d) \(y=\sqrt{25^x-5^x}\)
Hãy nêu các tính chất của hàm số lũy thừa ?
Bảng tóm tắt các tính chất của hàm số lũy thừa trên khoảng (0, +∞)
|
|
α > 0 |
α <0 |
|
Đạo hàm |
|
|
|
Chiều biến thiên |
Hàm số luôn đồng biến |
Hàm số luôn nghịch biến |
|
Tiệm cận |
Không có |
Tiệm cận ngang là Ox Tiệm cận đứng là Oy |
|
Đồ thị |
Đồ thị luôn đi qua điểm (1, 1) |
Hãy nêu các tính chất của lũy thừa với số mũ thực ?
Hãy nêu các tính chất của hàm số mũ và hàm số lôgarit ?
- Tính chất của hàm số mũ y= ax ( a > 0, a# 1).
- Tập xác định: .
- Đạo hàm: ∀x ∈ ,y’= axlna.
- Chiều biến thiên Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
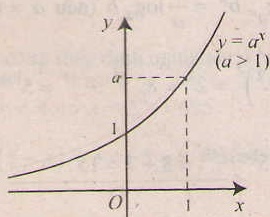
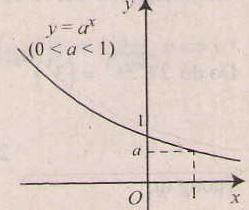
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).
- Tính chất của hàm số lôgarit y = logax (a> 0, a# 1).
- Tập xác định: (0; +∞).
- Đạo hàm ∀x ∈ (0; +∞),y’ = .
- Chiều biến thiên: Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
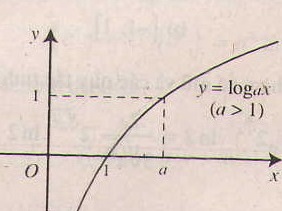
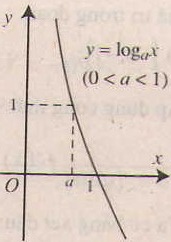
Giải các phương trình :
a) \(3^{x+4}+3.5^{x+3}=5^{x+4}+3^{x+3}\)
b) \(25^x-6.5^x+5=0\)
c) \(4.9^x+12^x-3.16^x=0\)
d) \(\log_7\left(x-1\right)\log_7x=\log_7x\)
e) \(\log_3x+\log_{\sqrt{3}}x+\log_{\dfrac{1}{3}}x=6\)
f) \(\log\dfrac{x+8}{x-1}=\log x\)

Trả lời bởi Nguyen Thuy Hoa