a) Hàm số \(y=\cos3x\) có phải là hàm số chẵn không ? Tại sao ?
b) Hàm số \(y=\tan\left(x+\dfrac{\pi}{5}\right)\) có phải là hàm số lẻ không ? Tại sao ?
Căn cứ vào đồ thị hàm số \(y=\sin x\), tìm những giá trị của x trên đoạn \(\left[-\dfrac{3\pi}{2};2\pi\right]\) để hàm số đó :
a) Nhận giá trị bằng -1
b) Nhận giá trị âm
Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
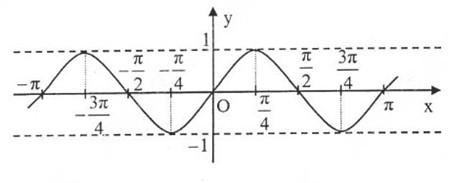
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)
Tìm giá trị lớn nhất của các hàm số sau :
a) \(y=\sqrt{2\left(1+\cos x\right)}+1\)
b) \(y=3\sin\left(x-\dfrac{\pi}{6}\right)-2\)
a) Ta có:
−1≤cosx≤1,∀x∈R⇔0≤1+cosx≤2⇔0≤2(1+cosx)≤4⇔1≤√2(1+cosx+1≤3−1≤cosx≤1,∀x∈R⇔0≤1+cosx≤2⇔0≤2(1+cosx)≤4⇔1≤2(1+cosx+1≤3
Vậy y ≤ 3, ∀ x ∈ R
Dấu “ = “ xảy ra ⇔ cos x = 1 ⇔ x = k2π (k ∈ Z)
Vậy ymax = 3 khi x = k2π
b) Ta có:
Với mọi x ∈ R, ta có:
sin(x−π6)≤1⇔3sin(x−π6)≤3⇔3sin(x−π6)−2≤1⇔y≤1sin(x−π6)≤1⇔3sin(x−π6)≤3⇔3sin(x−π6)−2≤1⇔y≤1
Vậy ymax = 1 khi sin(x−π6)=1⇔x=2π3+k2π,k∈Z
Giải các phương trình sau :
a) \(\sin\left(x+1\right)=\dfrac{2}{3}\)
b) \(\sin^22x=\dfrac{1}{2}\)
c) \(\cot^2\dfrac{x}{2}=\dfrac{1}{3}\)
d) \(\tan\left(\dfrac{\pi}{12}+12x\right)=-\sqrt{3}\)
a) Ta có:
sin(x+1)=23⇔[x+1=arcsin23+k2πx+1=π−arcsin23+k2π⇔[x=−1+arcsin23+k2πx=−1+π−arcsin23+k2π;k∈Zsin(x+1)=23⇔[x+1=arcsin23+k2πx+1=π−arcsin23+k2π⇔[x=−1+arcsin23+k2πx=−1+π−arcsin23+k2π;k∈Z
b) Ta có:
sin22x=12⇔1−cos4x2=12⇔cos4x=0⇔4x=π2+kπ⇔x=π8+kπ4,k∈Zsin22x=12⇔1−cos4x2=12⇔cos4x=0⇔4x=π2+kπ⇔x=π8+kπ4,k∈Z
c) Ta có:
cot2x2=13⇔⎡⎢⎣cotx2=√33(1)cotx2=−√33(2)(1)⇔cotx2=cotπ3⇔x2=π3+kπ⇔x=2π3+k2π,k∈z(2)⇔cotx2=cot(−π3)⇔x2=−π3+kπ⇔x=−2π3+k2π;k∈Zcot2x2=13⇔[cotx2=33(1)cotx2=−33(2)(1)⇔cotx2=cotπ3⇔x2=π3+kπ⇔x=2π3+k2π,k∈z(2)⇔cotx2=cot(−π3)⇔x2=−π3+kπ⇔x=−2π3+k2π;k∈Z
d) Ta có:
tan(π12+12x)=−√3⇔tan(π12+12π)=tan(−π3)⇔π12+12=−π3+kπ⇔x=−5π144+kπ12,k∈Z
Vậy nghiệm của phương trình đã cho là: x=−5π144+kπ12,k∈Z
Giải các phương trình sau :
a) \(2\cos^2x-3\cos x+1=0\)
b) \(25\sin^2x+15\sin2x+9\cos^2x=25\)
c) \(2\sin x+\cos x=1\)
d) \(\sin x+1,5\cot x=0\)
a) 2cos2x - 3cosx + 1 = 0 (1)
Đặt : t = cosx với điều kiện -1 \(\le t\le1\)
(1)\(\Leftrightarrow\) 2t2 - 3t + 1= 0
\(\Leftrightarrow\left[{}\begin{matrix}t=1\\t=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}=cosx\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\left(k\in Z\right)}\)
Trả lời bởi Tuyết Nhi MelodyTìm tập xác định của các hàm số
a) \(y=\dfrac{2-\cos x}{1+\tan\left(x-\dfrac{\pi}{3}\right)}\)
b) \(y=\dfrac{\tan x+\cot x}{1-\sin2x}\)
Xác định tính chẵn lẻ của các hàm số :
a) \(y=\sin^3x-\tan x\)
b) \(y=\dfrac{\cos x+\cot^2x}{\sin x}\)
Chia các đoạn sau thành hai đoạn, trên một đoạn hàm số \(y=\sin x\) tăng, còn trên đoạn kia hàm số đó giảm :
a) \(\left[\dfrac{\pi}{2};2\pi\right]\)
b) \(\left[-\pi;0\right]\)
c) \(\left[-2\pi;-\pi\right]\)
a) Hàm số \(y=\sin x\) giảm trên đoạn \(\left[\dfrac{\pi}{2};\dfrac{3\pi}{2}\right]\) và tăng trên đoạn \(\left[\dfrac{3\pi}{2};2\pi\right]\)
b) \(y=\sin x\) giảm trên \(\left[-\pi;-\dfrac{\pi}{2}\right]\), tăng trên \(\left[-\dfrac{\pi}{2};0\right]\)
c) \(y=\sin x\) tăng trên \(\left[-2\pi;-\dfrac{3\pi}{2}\right]\), giảm trên \(\left[-\dfrac{3\pi}{2};-\pi\right]\)
Trả lời bởi Nguyen Thuy HoaTìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số :
a) \(y=3-4\sin x\)
b) \(y=2-\sqrt{\cos x}\)
a) Do \(-1\le sinx\le1,\forall x\in R\).
Nên giá trị lớn nhất của \(y=3-4sinx\) bằng \(3-4.\left(-1\right)=7\)khi \(sinx=-1\)\(\Leftrightarrow x=-\dfrac{\pi}{2}+k\pi\).
Giá trị nhỏ nhất của \(y=3-4sinx\) bằng \(3-4.1=-1\) đạt được khi \(sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\).
Vẽ đồ thị của các hàm số :
a) \(y=\sin2x+1\)
b) \(y=\cos\left(x-\dfrac{\pi}{6}\right)\)
a) Đồ thị của hàm số \(y=\sin2x+1\) thu được từ đồ thị hàm số \(y=\sin2x\) bằng cách tịnh tiến song song với trục tung lên phía trên một đơn vị
b) Đồ thị hàm số \(y=\cos\left(x-\dfrac{\pi}{6}\right)\) thu được từ đồ thị hàm số \(y=\cos x\) bằng cách tịnh tiến song song với trục hoành sang phải một đoạn bằng \(\dfrac{\pi}{6}\)
Trả lời bởi Nguyen Thuy Hoa
a) Ta có:
- Hàm số y = cos 3x có tập xác định là D = R
- ∀ x ∈ D ⇒ - x ∈ D
- và f(-x) = cos 3(-x) = cos (-3x) = cos(3x) = f(x)
Vậy hàm số y = cos 3x là hàm số chẵn
b)
Ta có:
Hàm số \(y=tan\left(x+\dfrac{\pi}{5}\right)\) không là hàm số lẻ vì:
\(y=tan\left(x+\dfrac{\pi}{5}\right)\) có tập xác định là \(D=R\backslash\left\{\dfrac{3\pi}{10}+k\pi\right\}\).
Mà với mọi x ∈ D, ta không suy ra được -x ∈ D
Chẳng hạn:
Lấy \(x=-\dfrac{3\pi}{10}\in D\). Ta có \(-x=\dfrac{3\pi}{10}\notin D\).
Vậy hàm số \(y\left(x\right)\) có tập xác định không tự đối xứng nên \(y=tan\left(x+\dfrac{\pi}{5}\right)\) không là hàm số lẻ.
Trả lời bởi Lê Thiên Anh