Mỗi khẳng định sau đúng hay sai? Vì sao?
a) \(0,01=\sqrt{0,0001};\)
b) \(-0,5=\sqrt{-0,25};\)
c) \(\sqrt{39}< 7\) và \(\sqrt{39}>6;\)
d) \(\left(4-\sqrt{13}\right).2x< \sqrt{3}\left(4-\sqrt{13}\right)\Leftrightarrow2x< \sqrt{3}.\)
Mỗi khẳng định sau đúng hay sai? Vì sao?
a) \(0,01=\sqrt{0,0001};\)
b) \(-0,5=\sqrt{-0,25};\)
c) \(\sqrt{39}< 7\) và \(\sqrt{39}>6;\)
d) \(\left(4-\sqrt{13}\right).2x< \sqrt{3}\left(4-\sqrt{13}\right)\Leftrightarrow2x< \sqrt{3}.\)
Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1 cm, cho bốn điềm M, N, P, Q (h.3)
Hãy xác định số đo cạnh, đường chéo và diện tích tứ giác MNPQ.
Tứ giác MNPQ có:
- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 2cm, chiều rộng 1cm. Do đó theo định lí Py-ta-go:
.
- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 3cm, chiều rộng 1cm nên độ dài đường chéo là:
Từ các kết quả trên suy ra MNPQ là hình vuông. Vậy diện tích tứ giác MNPQ bằng .
Tính:
a. \(\sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01};\) b. \(\sqrt{1,44.1,21-1,44.0,4};\)
c. \(\sqrt{\dfrac{165^2-124^2}{164}};\) d. \(\sqrt{\dfrac{149^2-76^2}{457^2-384^2}}.\)
Tìm x biết:
a. \(\sqrt{\left(x-3\right)^2}=9;\) b. \(\sqrt{4x^2+4x+1}=6.\)
a) \(\sqrt{\left(x-3\right)^2}=9\)
\(\Leftrightarrow\sqrt{\left(x-3\right)^2}^2=9^2\)
\(\Leftrightarrow\left(x-3\right)^2=81\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=9\\x-3=-9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-6\end{matrix}\right.\)
b) \(\sqrt{4x^2+4x+1}=6\)
\(\Leftrightarrow\sqrt{4x^2+4x+1}^2=6^2\)
\(\Leftrightarrow4x^2+4x+1-36=0\)
\(\Leftrightarrow4x^2+4x-35=0\)
\(\Leftrightarrow4\cdot\left(x-\dfrac{5}{2}\right)\cdot\left(x+\dfrac{7}{2}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-\dfrac{5}{2}=0\\x+\dfrac{7}{2}=0\end{matrix}\right.\rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Trả lời bởi Đức MinhGiải phương trình:
a. \(\sqrt{2}.x-\sqrt{50}=0;\) b. \(\sqrt{3}.x+\sqrt{3}=\sqrt{12}+\sqrt{27};\)
c. \(\sqrt{3}.x^2-\sqrt{12}=0;\) d. \(\dfrac{x^2}{\sqrt{5}}-\sqrt{20}=0.\)
a, \(\sqrt{2}x-\sqrt{50}=0\Leftrightarrow\sqrt{2}x-5\sqrt{2}=0\Leftrightarrow\sqrt{2}\left(x-5\right)=0\Leftrightarrow x=5\)
b, \(\sqrt{3}x+\sqrt{3}=\sqrt{12}+\sqrt{27}\Leftrightarrow\sqrt{3}\left(x+1\right)=5\sqrt{3}\Leftrightarrow x+1=5\Leftrightarrow x=4\)
c, \(\sqrt{3}x^2-\sqrt{12}=0\Leftrightarrow\sqrt{3}\left(x^2-2\right)=0\Leftrightarrow x^2-2=0\Leftrightarrow x=\pm\sqrt{2}\)
d, \(\dfrac{x^2}{\sqrt{5}}-\sqrt{20}=0\Leftrightarrow\dfrac{1}{\sqrt{5}}\left(x^2-10\right)=0\Leftrightarrow x^2-10=0\Leftrightarrow x=\pm\sqrt{10}\)
Trả lời bởi ¨°o.O♫♀¤♪ Zin Phan ♪¤♂♫O...a. So sánh \(\sqrt{25-16}\) và \(\sqrt{25}-\sqrt{16};\)
b. Chứng minh rằng, với a > b > 0 thì \(\sqrt{a}-\sqrt{b}< \sqrt{a-b}.\)
a) HD: Thực hiện phép khai căn rồi so sánh kết quả.
Trả lời: > √25 - √16;.
b) HD: Ta có thể chứng minh rằng √a < + √b.
Nhưng điều này suy ra từ kết quả bài tập 26.b) SGK nếu lưu ý rằng
√a = .
Tính:
a. \(\dfrac{\sqrt{2}}{\sqrt{18}};\) b. \(\dfrac{\sqrt{15}}{\sqrt{735}};\) c. \(\dfrac{\sqrt{12500}}{\sqrt{500}};\) d. \(\dfrac{\sqrt{6^5}}{\sqrt{2^3.3^5}}.\)
a.\(\dfrac{\sqrt{2}}{\sqrt{18}}=\sqrt{\dfrac{2}{18}}=\sqrt{\dfrac{1}{9}}=\dfrac{1}{3}\)
b.\(\dfrac{\sqrt{15}}{\sqrt{735}}=\sqrt{\dfrac{15}{735}}=\sqrt{\dfrac{1}{49}}=\dfrac{1}{7}\)
c.\(\dfrac{\sqrt{12500}}{\sqrt{500}}=\sqrt{\dfrac{12500}{500}}=\sqrt{25}=5\)
d.\(\dfrac{\sqrt{6^5}}{\sqrt{2^3.33^5}}=\sqrt{\dfrac{2^5.3^5}{2^3.3^5}}=\sqrt{2^2}=2\)
Trả lời bởi Bùi Nhất DuyTính:
a. \(\sqrt{\dfrac{289}{225}};\) b. \(\sqrt{2\dfrac{14}{25}};\) c. \(\sqrt{\dfrac{0,25}{9}};\) d. \(\sqrt{\dfrac{8,1}{1,6}}.\)
Rút gọn các biểu thức sau:
a. \(\dfrac{y}{x}.\sqrt{\dfrac{x^2}{y^4}}\) với x > 0; \(y\ne0;\) b. \(2y^2.\sqrt{\dfrac{x^4}{4y^2}}\) với y < 0;
c. \(5xy.\sqrt{\dfrac{25x^2}{y^6}}\) với x < 0, y > 0; d. \(0,2x^3y^3.\sqrt{\dfrac{16}{x^4y^8}}\) với \(x\ne0;y\ne0.\)
a) =
.
=
.
=
vì x > 0.
Do đó =
.
b) =
.
=
.
.
Vì y < 0 nên │y│= -y. Do đó =
.
=
.
c) 5xy. = 5xy.
= 5xy.
.
Vì x < 0, y > 0 nên = -x và
=
.
Do đó: 5xy = 5xy.
= -
.
d) 0,2 =
= 0,2
=
Nếu x > 0 thì > 0 nên
. Do đó 0,2
=
.
Nếu x < 0 thì < 0 nên
. Do đó 0,2
= -
.
Rút gọn các biểu thức sau:
a. \(ab^2.\sqrt{\dfrac{3}{a^2b^4}}\) với a < 0, \(b\ne0;\) b. \(\sqrt{\dfrac{27\left(a-3\right)^2}{48}}\) với a > 3;
c. \(\sqrt{\dfrac{9+12a+4a^2}{b^2}}\) với \(a\ge-1,5\) và b < 0;
d. \(\left(a-b\right).\sqrt{\dfrac{ab}{\left(a-b\right)^2}}\) với a < b <0.
a,\(ab^2\sqrt{\dfrac{3}{a^2b^4}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}=ab^2.\dfrac{\sqrt{3}}{ab^2}=\sqrt{3}\)
b,\(\sqrt{\dfrac{27\left(a-3\right)^2}{48}}=\dfrac{3\sqrt{3}\left(a-3\right)}{4\sqrt{3}}=\dfrac{3}{4}\left(a-3\right)\)
c,\(\sqrt{\dfrac{9+12a+4a^2}{b^2}}=\dfrac{\sqrt{\left(3+2a\right)^2}}{\sqrt{b^2}}=\dfrac{3+2a}{b}\)
d, \(\left(a-b\right).\sqrt{\dfrac{ab}{\left(a-b\right)^2}}=\left(a-b\right).\dfrac{\sqrt{ab}}{\sqrt{\left(a-b\right)^2}}=\left(a-b\right).\dfrac{\sqrt{ab}}{\left(a-b\right)}=\sqrt{ab}\)
Trả lời bởi ¨°o.O♫♀¤♪ Zin Phan ♪¤♂♫O...
a) Đúng
b) Sai. Số âm không có căn bậc hai.
c) Đúng vì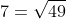 và
và 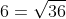 .
.
d) Đúng vì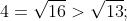 do đó
do đó 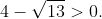
Trả lời bởi qwerty