Vì a ≥ 0 nên a xác định, b ≥ 0 nên b xác định
Ta có: a - b 2 ≥ 0 ⇒ a - 2 a b + b ≥ 0 ⇒ a + b ≥ 2 a b
⇒ a + b + a + b ≥ a + b + 2 a b
⇒ 2(a + b) ≥ a 2 + 2 a b + b 2
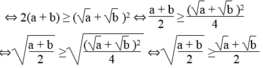
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Chứng minh rằng với a+b>c và |a-b|<c với a,b,c >0 thì phương trình bậc hai a^2x^2 +(a^2+b^2-c^2)x +b^2=0 vô nghiệm
ĐOẠN MK BÔI ĐỎ GIẢI THÍCH HỘ
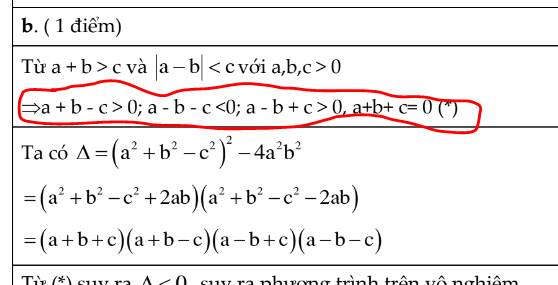
chứng minh rằng a^2/b^2+b^2/a^2> =2 ( a khác 0 và b khác 0)
ai giúp mình với
cho 1/a+1/b+1/c=0 với a,b,c khác 0 và M=b^2c^2/a+c^2a^2/b+a^2b^2/c. chứng minh M=3abc
giúp mình với. cám ơn nhiều
cho P=\(\dfrac{4}{a^2+b^2}+\dfrac{1}{ab}\),với a;b>0 và a+b=\(\sqrt{2}\). chứng minh P≥(\(\sqrt{2}+1\))\(^2\)
cho a>0,b>0 và ab=1.chứng minh:
\(\dfrac{a}{a^4+b^2}+\dfrac{b}{a^2+b^4}\)\(\le\)1
So sánh
Với a>0 và b>0, chứng minh a + b < a + b
H24
1 tháng 11 2023 lúc 19:16
Chứng minh \(\sqrt{a^{2} +b^{2} }\) ≥ \(\dfrac{a +b}{\sqrt{2}}\) với mọi a; b ≥ 0.
Cho 0 ≤a;b;c ≤2 và a-b;b-c;c-a khác 0. Chứng minh rằng: 1/(a-b)^2 + 1/(b-c)^2 +1/(c-a)^2 ≥9/4
Chứng minh : 1/a +1/b >= 2 biết a+b =< 2 và a>0; b>0
Cho 2 số a và b chứng minh a + b > 0 . Biết rằng a , b > 0