a. Em tự giải
b.
Xét hai tam giác ADB và ABE có:
\(\left\{{}\begin{matrix}\widehat{DAB}-chung\\\widehat{ABD}=\widehat{AEB}\left(\text{cùng chắn BD}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ADB\sim\Delta ABE\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AB}{AE}\Rightarrow AB^2=AD.AE\) (1)
Theo t/c hai tiếp tuyến cắt nhau: \(AB=AC\)
Lại có \(OB=OC=R\)
\(\Rightarrow OA\) là trung trực của BC
\(\Rightarrow\)OA vuông góc BC tại H
Áp dụng hệ thức lượng trong tam giác vuông ABO với đường cao BH:
\(AB^2=AH.AO\) (2)
(1);(2) \(\Rightarrow AH.AO=AD.AE\)
c.
Từ câu b \(\Rightarrow\dfrac{AD}{AO}=\dfrac{AH}{AE}\)
Xét hai tam giác ADH và AOE có:
\(\left\{{}\begin{matrix}\widehat{HAD}-chung\\\dfrac{AD}{AO}=\dfrac{AH}{AE}\end{matrix}\right.\) \(\Rightarrow\Delta ADH\sim\Delta AOE\left(c.g.c\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{OEA}\) (3)
Do \(OD=OE=R\Rightarrow\Delta ODE\) cân tại O
\(\Rightarrow\widehat{OEA}=\widehat{ODE}\)
\(\Rightarrow\widehat{AHD}=\widehat{ODE}\)
d.
Ta có: \(\widehat{AHD}+\widehat{OHD}=180^0\) (hai góc kề bù) (4)
(3);(4) \(\Rightarrow\widehat{OEA}+\widehat{OHD}=180^0\)
\(\Rightarrow OHDE\) nội tiếp hay O, H, D, E cùng thuộc 1 đường tròn (5)
Do K là giao điểm 2 tiếp tuyến tại D và E \(\Rightarrow\widehat{OEK}=\widehat{ODK}=90^0\)
\(\Rightarrow\) D và E cùng nhìn OK dưới 1 góc vuông nên O, E, D, K cùng thuộc đường tròn đường kính OK (6)
(5);(6) \(\Rightarrow O,H,D,K,E\) cùng thuộc đường tròn đường kính OK
\(\Rightarrow\widehat{OHK}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{OHK}=90^0\)
Hay \(KH\perp OA\) tại H
Mà theo cmt ta có \(AB\perp OA\) tại H
\(\Rightarrow\) Hai đường thẳng KH và AB trùng nhau
Hay K thuộc đường thẳng AB
Vậy khi D di chuyển trên cung BC thì K di chuyển trên đường thẳng AB cố định


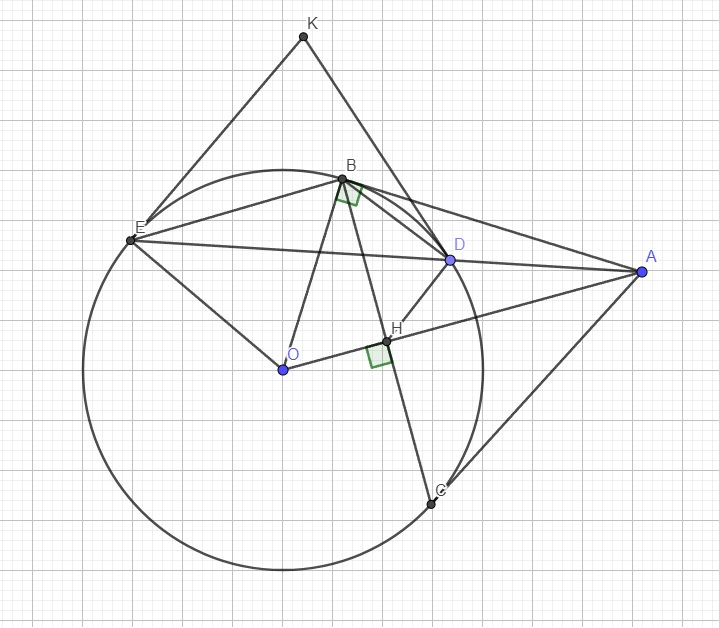
 vẽ hình luôn ạ
vẽ hình luôn ạ



