vẽ hình + giải
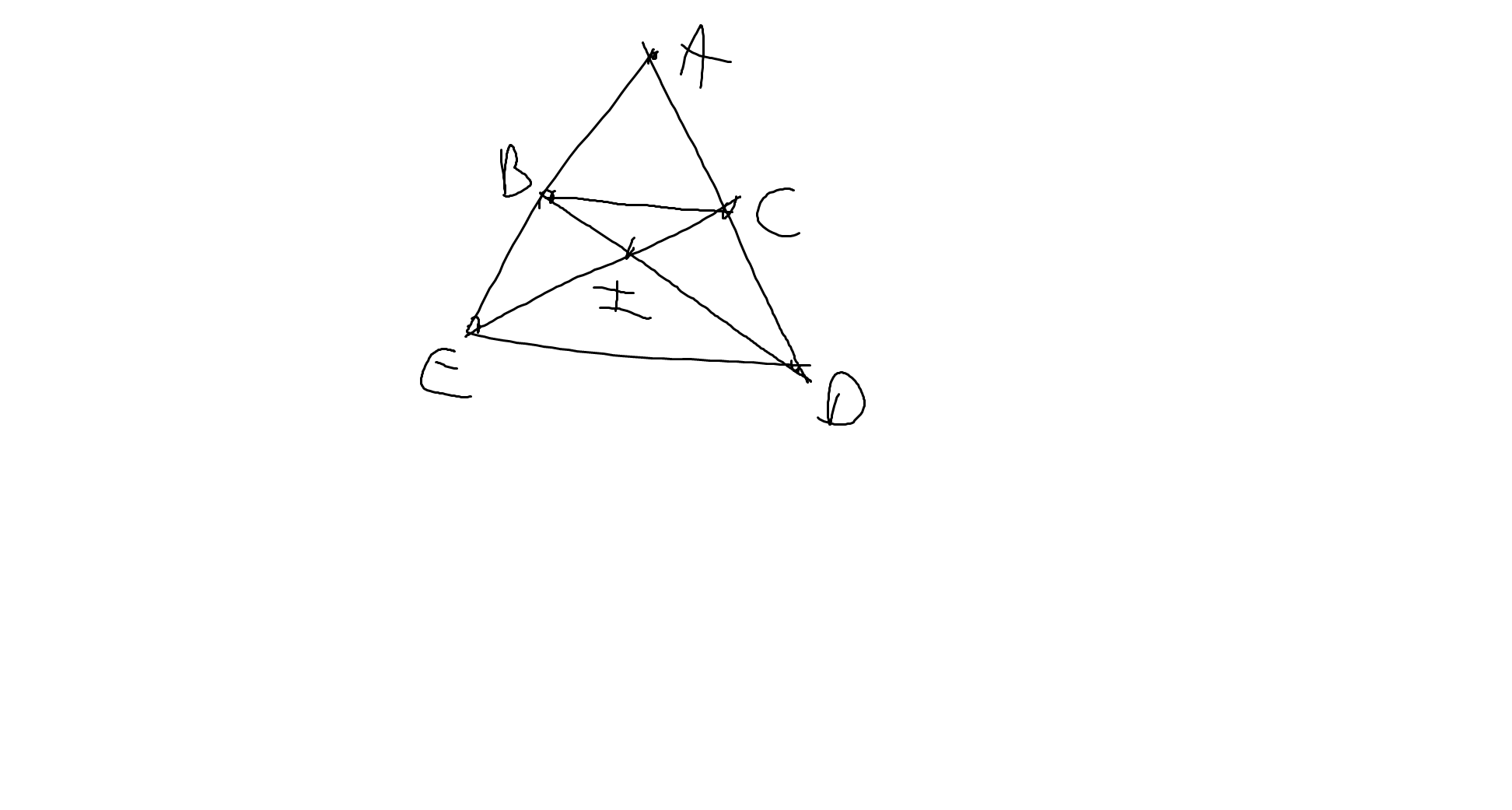
a: Xét ΔABD vuông tại B và ΔACE vuông tại C có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
=>AD=AE và BD=CE
b: Xét ΔABI vuông tại B và ΔACI vuông tại C có
AI chung
AB=AC
Do đó: ΔABI=ΔACI
=>IB=IC
Ta có: IB+ID=BD
IC+IE=CE
mà IB=IC và BD=CE
nên ID=IE
ΔIAB=ΔIAC
=>\(\widehat{BAI}=\widehat{CAI}\)
c: Xét ΔAED có \(\dfrac{AB}{AE}=\dfrac{AC}{AD}\)
nên BC//ED
Ta có: AD=AE
=>A nằm trên đường trung trực của DE(1)
Ta có: ID=IE
=>I nằm trên đường trung trực của DE(2)
Từ (1),(2) suy ra AI là đường trung trực của DE
=>AI\(\perp\)DE
d: ΔCED vuông tại C
=>\(\widehat{CIE}+\widehat{CDE}=90^0\)
=>\(\widehat{CDE}=90^0-30^0=60^0\)
Ta có: BC//DE
=>\(\widehat{ACB}=\widehat{ADE}\)(hai góc đồng vị)
=>\(\widehat{ACB}=60^0\)
Vậy: Để \(\widehat{IED}=30^0\) thì ΔABC cần có thêm điều kiện là \(\widehat{ACB}=60^0\)
