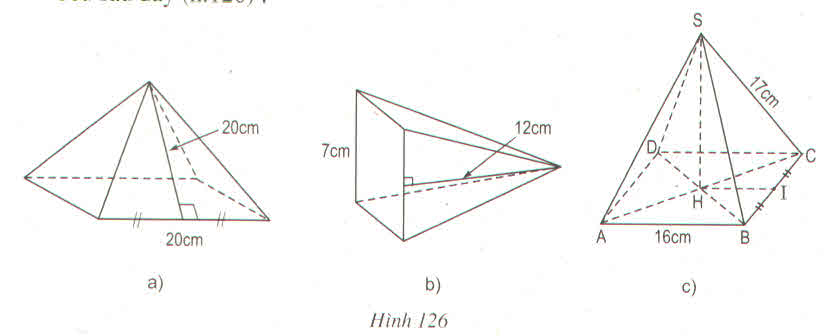
Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau ?
b) Sử dụng định lí Pi-ta-go để tính chiều cao ứng với đáy của mỗi tam giác
c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu ?
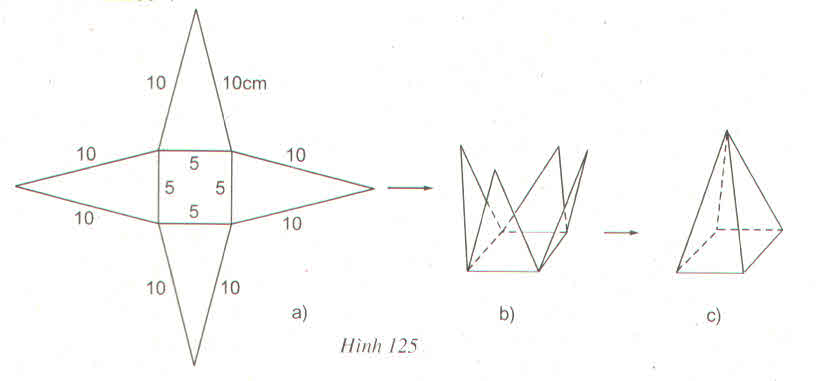
a) Trong hình 125a có 4 tam giác cân bằng nhau.
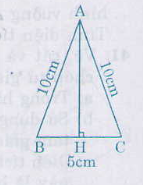
b) Chiều cao ứng với đáy của mỗi tam giác:
\(AH=\sqrt{AC^2-HC^2}\)
\(=\sqrt{AC^2-\left(\dfrac{1}{2}.5\right)^2}=\sqrt{100-\dfrac{25}{4}}=9,68\left(cm\right)\)
c) Diện tích xung quanh hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).5.4.9,68 = 96,8 (cm2 )
Diện tích đáy:
Sđ = 52 = 25 (cm2 )
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 121,8 (cm2 )