Bài 1: Hình hộp chữ nhật

1. Hình hộp chữ nhật.

Cho hình vẽ:

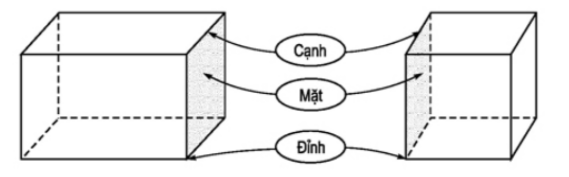
Hình vẽ trên cho ta hình ảnh của hình hộp chữ nhật.

- Hình hộp chữ nhật có 6 mặt, 8 đỉnh và 12 cạnh.

- Hình hộp chữ nhật có 6 mặt đều là các hình chữ nhật.

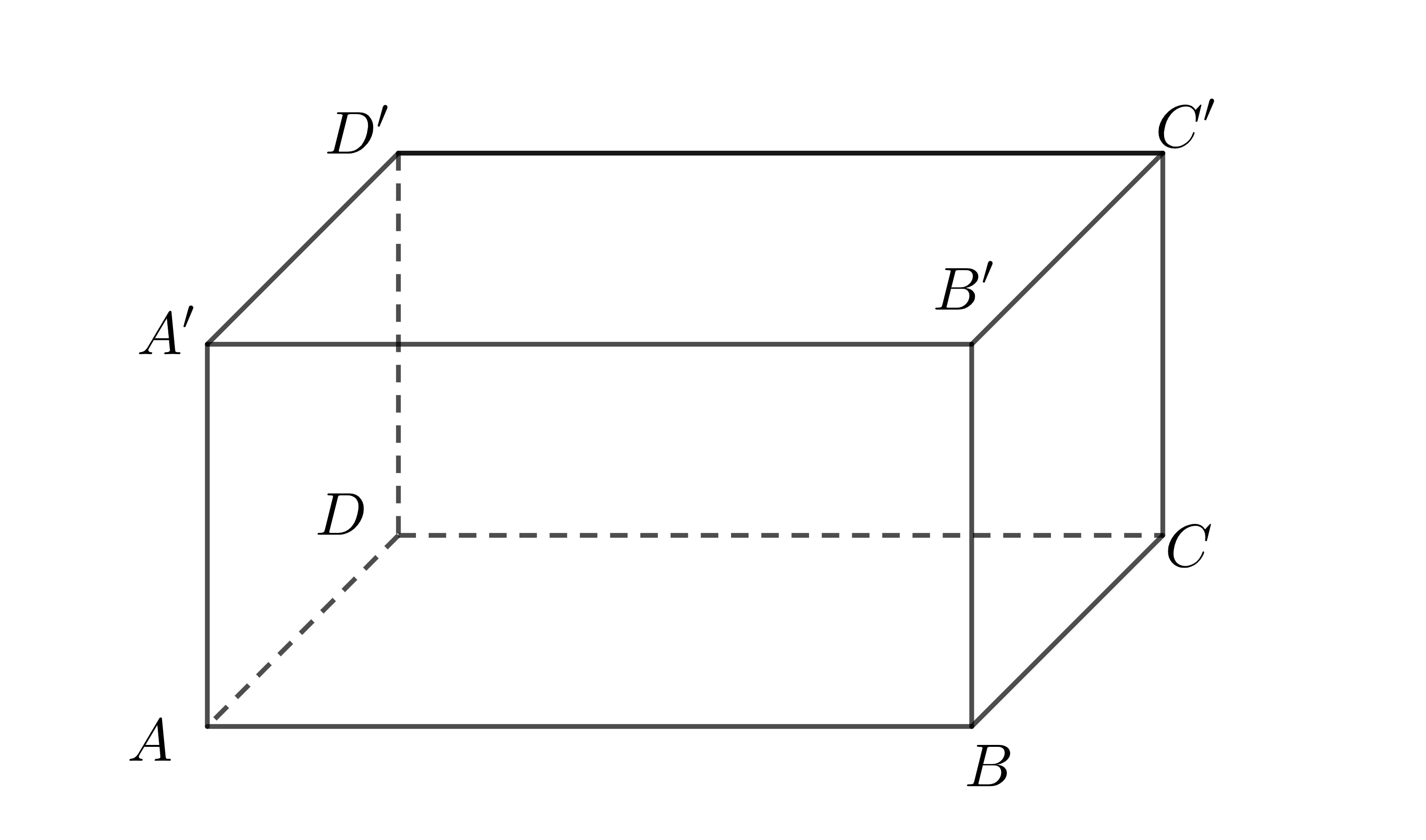
Ví dụ: Hình hộp chữ nhật \(ABCD.A'B'C'D'\) có:

       - 6 mặt là: \(\left(ABCD\right)\), \(\left(A'B'C'D'\right)\), \(\left(ABB'A'\right)\), \(\left(BCC'B'\right)\), \(\left(CDD'C'\right)\), \(\left(ADD'A'\right)\) đều là các hình chữ nhật.

       - 8 đỉnh là: \(A,B,C,D,A',B',C',D'\).

       - 12 cạnh là: \(AB,BC,CD,DA,A'B',B'C',C'D',D'A',AA',BB',CC',DD'\)

- Hai mặt của hình hộp chữ nhật không có điểm chung được gọi là hai mặt đối diện và có thể xem chúng là hai mặt đáy của hình hộp chữ nhật, khi đó các mặt còn lại của hình hộp chữ nhật được gọi là các mặt bên.

Ví dụ: Xét trong hình hộp chữ nhật \(ABCD.A'B'C'D'\):

    +) Các cặp mặt đối diện của hình hộp chữ nhật là: \(\left(ABCD\right)\) và \(\left(A'B'C'D'\right)\), \(\left(ABB'A'\right)\) và \(\left(CDD'C'\right)\), \(\left(BCC'B'\right)\) và \(\left(ADD'A'\right)\)

Như vậy:

    +) Nếu xem \(\left(ABCD\right)\) và \(\left(A'B'C'D'\right)\) là hai mặt đáy thì 4 mặt còn lại là \(\left(ABB'A'\right)\), \(\left(BCC'B'\right)\), \(\left(CDD'C'\right)\) và\(\left(ADD'A'\right)\) là các mặt bên.

    +) Nếu xem \(\left(ABB'A'\right)\) và \(\left(CDD'C'\right)\) là hai mặt đáy thì 4 mặt còn lại là \(\left(BCC'B'\right)\), \(\left(ADD'A'\right)\), \(\left(ABCD\right)\) và \(\left(A'B'C'D'\right)\) là các mặt bên.

    +) Nếu xem \(\left(BCC'B'\right)\) và \(\left(ADD'A'\right)\)là hai mặt đáy thì 4 mặt còn lại là \(\left(ABCD\right)\), \(\left(A'B'C'D'\right)\), \(\left(ABB'A'\right)\), \(\left(CDD'C'\right)\) là các mặt bên.

- Hình lập phương là hình hộp chữ nhật có 6 mặt là các hình vuông.

Ví dụ hình lập phương \(EFGH.E'F'G'H'\):

2. Mặt phẳng và đường thẳng

Xét trong hình hộp chữ nhật \(ABCD.A'B'C'D'\), Ta có thể xem:

      - Các đỉnh: \(A,B,C,D,A',B',C',D'\) là các điểm;

      - Các cạnh \(AB,BC,CD,DA,A'B',B'C',C'D',D'A',AA',BB',CC',DD'\) là các đoạn thẳng;

      - Mỗi mặt (chẳng hạn mặt \(ABCD\)) là một phần của mặt phẳng (ta hình dung mặt phẳng trải rộng về mọi phía). 

Đường thẳng đi qua hai điểm \(A,B\) của mặt phẳng \(\left(ABCD\right)\) thì nằm trọn trong mặt phẳng đó (tức là mọi điểm của nó đều thuộc mặt phẳng).

Ví dụ: Xét trong hình hộp chữ nhật \(ABCD.A'B'C'D'\) , các mặt phẳng cùng chứa đường thẳng \(A'B'\) là:

           \(\left(A'B'C'D'\right)\),  \(\left(ABB'A'\right)\), \(\left(A'B'CD\right)\):