Bài 3: Thể tích hình hộp chữ nhật
Nội dung lý thuyết
Các phiên bản khác1. Đường thẳng vuông góc với mặt phẳng. Hai mặt phẳng vuông góc
Một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc một mặt phẳng không chứa nó thì nó vuông góc với mặt phẳng đó.
\(b\) và \(c\) cắt nhau và cùng thuộc \(mp\left(\alpha\right)\), \(a\) không thuộc \(mp\left(\alpha\right)\).
Nếu \(\left\{{}\begin{matrix}a\perp b\\a\perp c\end{matrix}\right.\) thì \(a\perp mp\left(\alpha\right)\)
Ví dụ: Xét trong hình hộp chữ nhật \(ABCD.A'B'C'D'\) (như hình vẽ)
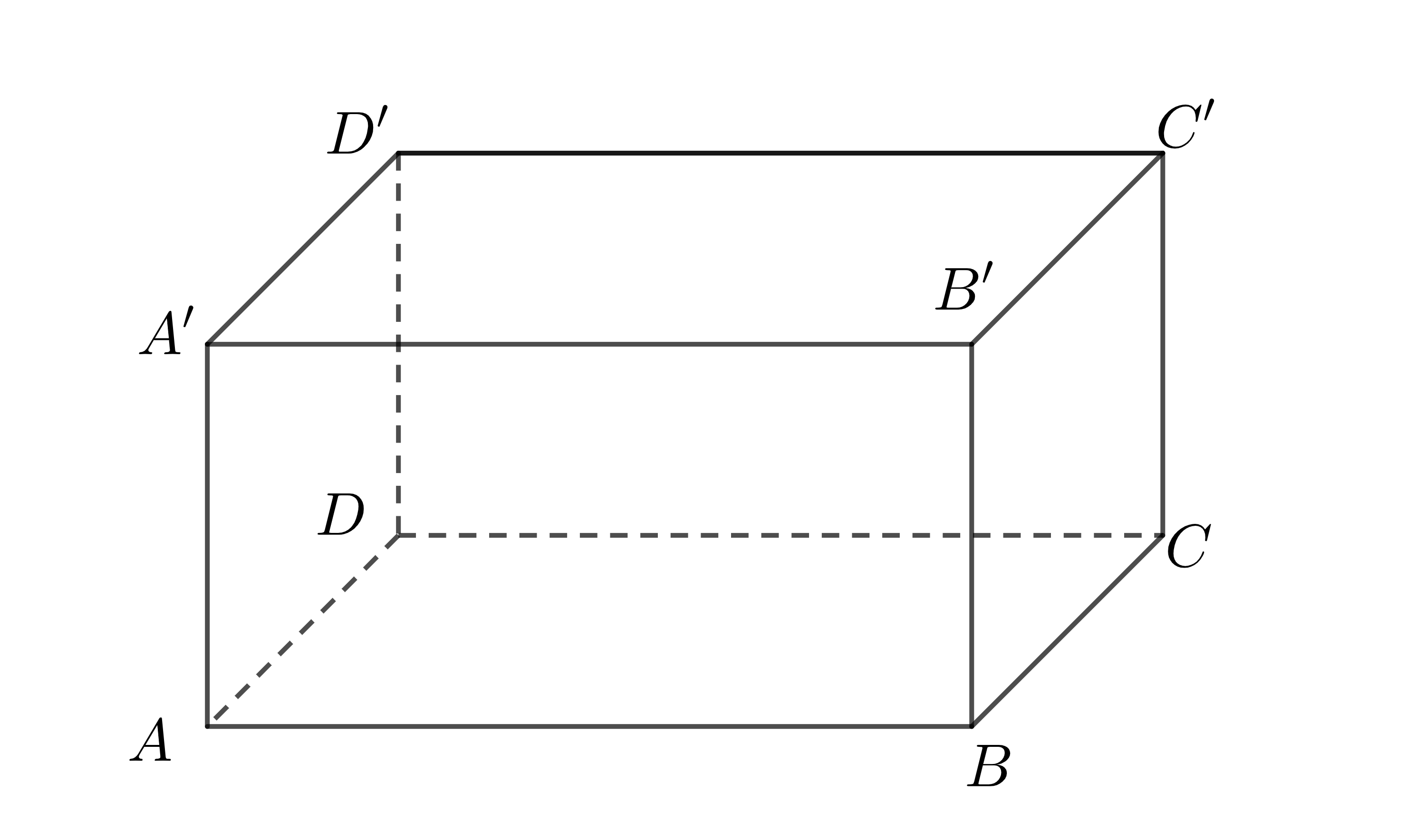
Ta nói đường thẳng \(AA'\) vuông góc với mặt phẳng \(\left(ABCD\right)\) do \(AA'\) vuông góc với hai đường thẳng cắt nhau \(AB\) và \(AD\) thuộc mặt phẳng \(\left(ABCD\right)\)
Kí hiệu: \(AA'\perp mp\left(ABCD\right)\)
Tương tự như vậy, xét trong hình hộp trên:
+) \(BB'\perp mp\left(ABCD\right)\) do \(BB'\perp AB\) và \(BB'\perp BC\)
+) \(CC'\perp mp\left(A'B'C'D'\right)\) do \(CC'\perp C'D'\) và \(CC'\perp B'C'\)
+) \(A'D'\perp mp\left(CDD'C'\right)\) do \(A'D'\perp C'D'\) và \(A'D'\perp DD'\)
+) \(AB\perp mp\left(ADD'A'\right)\) do \(AB\perp AD\) và \(AB\perp AA'\)
Ta có thể kể thêm rất nhiều đường thẳng vuông góc với mặt phẳng khác nữa.
- Nhận xét: Nếu một đường thẳng vuông góc với một mặt phẳng tại điểm \(A\) thì nó vuông góc với mọi đường thẳng đi qua \(A\) thuộc mặt phẳng đó.
Ví dụ: Trong hình hộp chữ nhật \(ABCD.A'B'C'D'\),
+) \(AA'\perp mp\left(ABCD\right)\) tại \(A\) thì nó vuông góc với các đường thẳng đi qua \(A\) và thuộc \(mp\left(ABCD\right)\) như: \(AB,AC,AD,...\)
+) \(AA'\perp mp\left(A'B'C'D'\right)\) tại \(A'\) thì nó vuông góc với các đường thẳng đi qua \(A'\) và thuộc \(mp\left(A'B'C'D'\right)\) như: \(A'B',A'C',A'D',...\)
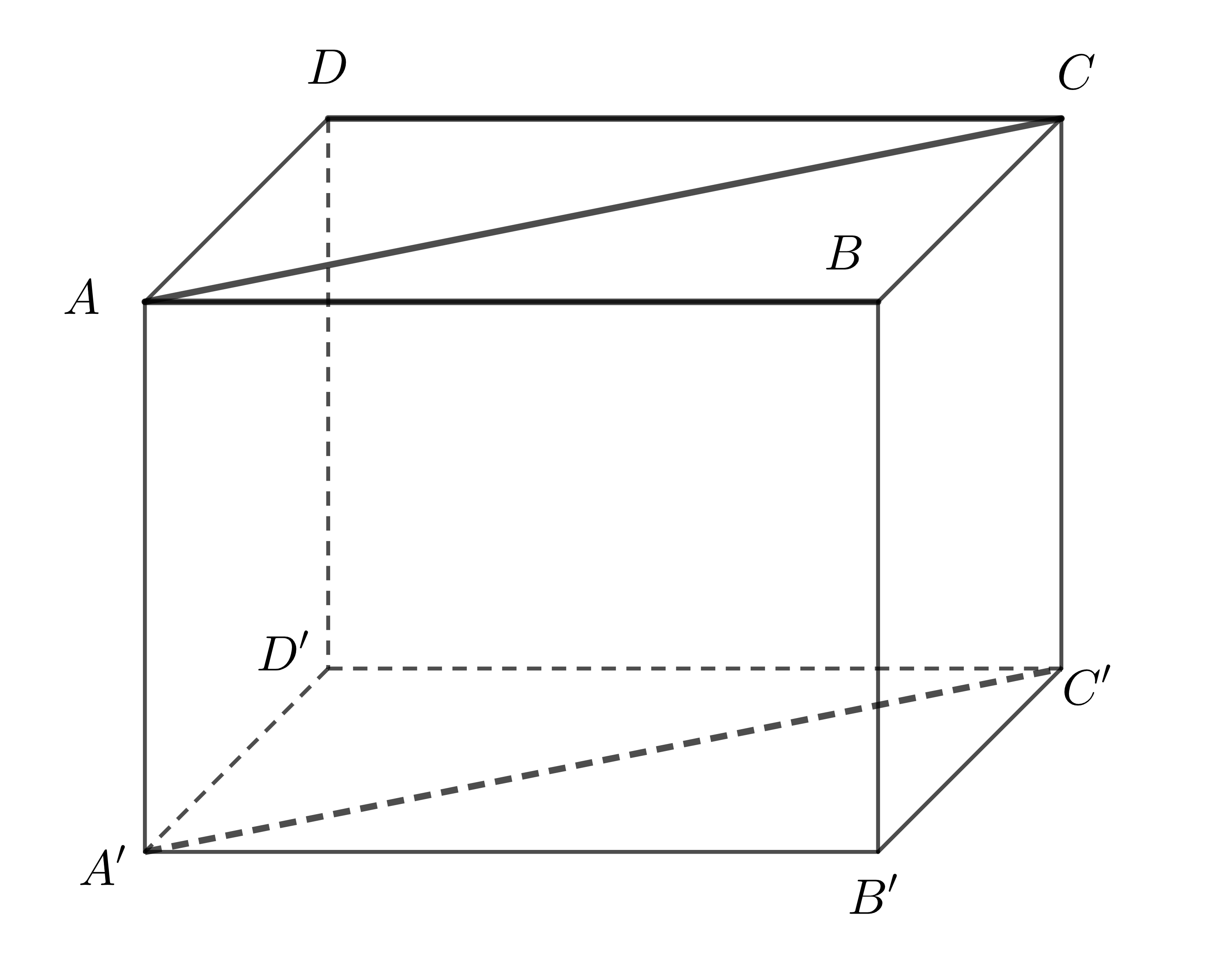
Ví dụ 1: Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(O,O'\) lần lượt là tâm của hình chữ nhật \(ABCD\) và \(A'B'C'D'\). Kể tên tất cả các đường thẳng vuông góc với mặt phẳng \(\left(ABCD\right)\)?
Giải:
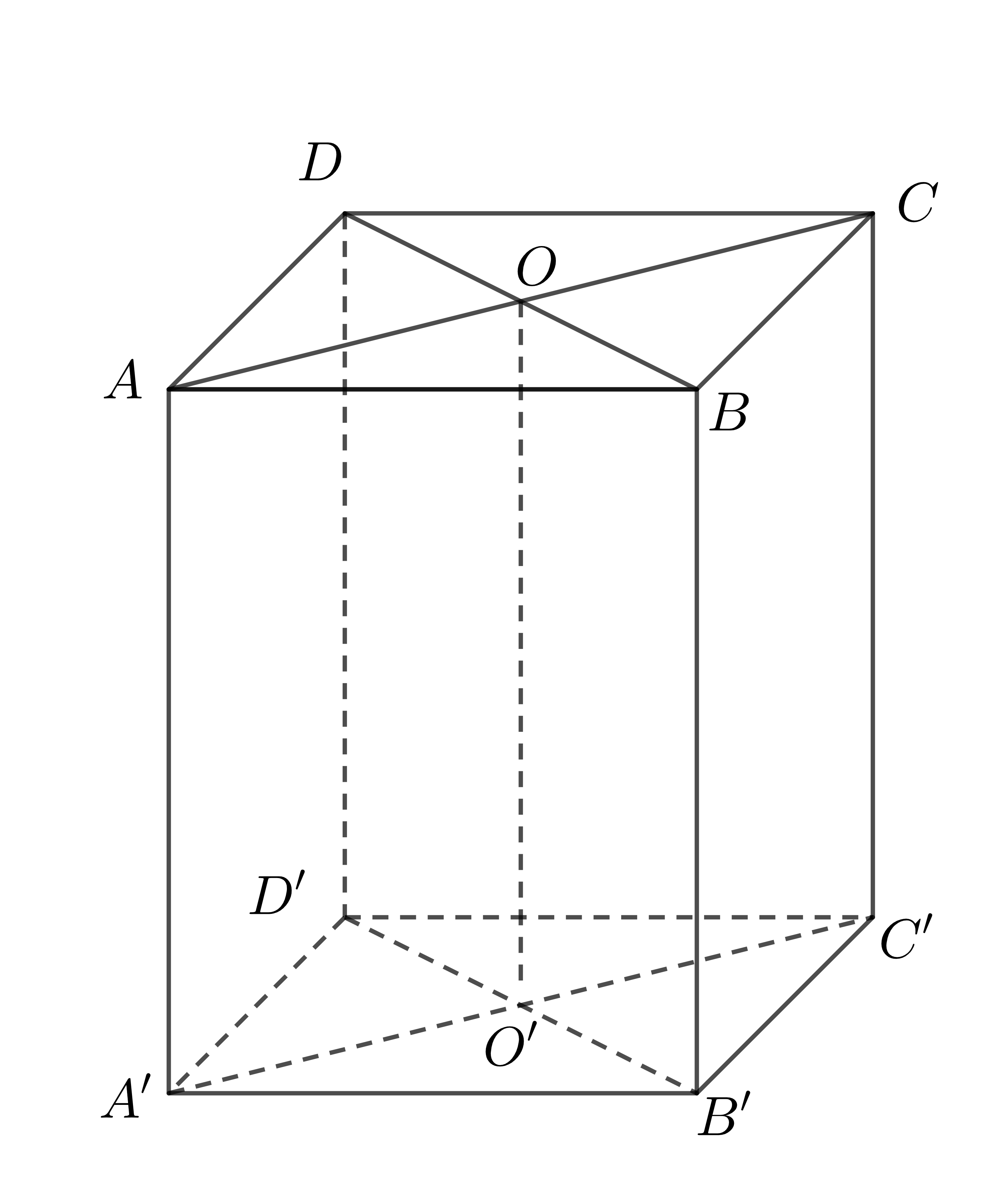
Như trên, ta đã chứng minh được \(AA'\perp mp\left(ABCD\right)\) ,\(BB'\perp mp\left(ABCD\right)\)
Ta có \(CC'\perp BC,CC'\perp CD\) nên \(CC'\perp mp\left(ABCD\right)\)
Ta có \(DD'\perp AD,DD'\perp CD\) nên \(DD'\perp mp\left(ABCD\right)\)
Lại có: \(AA'\perp mp\left(ABCD\right)\) nên \(AA'\perp AC\)
Tứ giác \(ACC'A\) là hình bình hành do \(AA'\)//\(CC'\) và \(AA'=CC'\) (do cùng bằng \(BB'\))
Mà \(AA'\perp AC\) nên \(ACC'A\) là hình chữ nhật
Do \(O,O'\) là tâm của 2 hình chữ nhật \(ABCD\) và \(A'B'C'D'\) nên \(O,O'\) là trung điểm của \(AC,A'C'\)
\(\Rightarrow OO'\)//\(AA'\)//\(CC'\) nên \(OO'\perp AC\)
Chứng minh tương tự ta cũng được \(OO'\perp BD\)
Suy ra \(OO'\perp mp\left(ABCD\right)\)
Vậy các đường thẳng vuông góc với \(mp\left(ABCD\right)\) trong hình hộp trên là: \(AA',BB',CC',DD',OO'\).
Khi một trong hai mặt phẳng chứa một đường thẳng v uông góc với mặt phẳng còn lại thì ta nói hai mặt phẳng đó vuông góc với nhau.
Nếu \(a\in mp\left(\alpha\right)\), \(a\perp mp\left(\beta\right)\) thì \(mp\left(\alpha\right)\perp mp\left(\beta\right)\)
Ví dụ:
+) Xét \(mp\left(ABCD\right)\) và \(mp\left(ABB'A'\right)\) có: \(\left\{{}\begin{matrix}AA'\in mp\left(ABB'A'\right)\\AA'\perp mp\left(ABCD\right)\end{matrix}\right.\) nên \(mp\left(ABCD\right)\perp mp\left(ABB'A'\right)\);
+) Xét \(mp\left(A'B'C'D'\right)\) và \(mp\left(CDD'C'\right)\) có \(\left\{{}\begin{matrix}CC'\in mp\left(CDD'C'\right)\\CC'\perp mp\left(A'B'C'D'\right)\end{matrix}\right.\) nên \(mp\left(CDD'C\right)\perp mp\left(A'B'C'D'\right)\);
+) Xét \(mp\left(ABB'A'\right)\) và \(mp\left(BCC'B'\right)\) có \(\left\{{}\begin{matrix}AB\in mp\left(ABB'A'\right)\\AB\perp mp\left(BCC'B'\right)\end{matrix}\right.\) nên \(mp\left(ABB'A'\right)\perp mp\left(BCC'B'\right)\);....
Tương tự như vậy ta có thể kể thêm nhiều cặp mặt phẳng vuông góc khác.
@1558241@@59595@
2. Thể tích hình hộp chữ nhật
Tổng quát:
Nếu hình hộp chữ nhật có các kích thước là \(a,b,c\) (cùng đơn vị đo) thì thể tích hình hộp chữ nhật đó là:
\(V=abc\)
Ví dụ 1: Một chiếc hộp dạng hình hộp chữ nhật có chiều dài là \(12cm\), chiều rộng là \(8cm\), chiều cao là \(1,5dm\). Tính thể tích chiếc hộp?
Giải:
Đổi \(1,5dm=15cm\)
Thể tích chiếc hộp là: \(12.8.15=1440\left(cm^3\right)\).
Ví dụ 2: Một bể nước hình hộp chữ nhật có chiều dài là \(2m\), chiều rộng là \(1,5m\), chiều cao gấp \(1,5\) lần chiều dài. Người ta bơm nước vào bể sao cho mực nước cao đến \(\dfrac{2}{3}\) chiều cao bể. Tính thể tích nước đã bơm vào bể? (Biết lúc đầu bể cạn)
Giải:
Chiều cao bể là: \(2.1,5=3\left(m\right)\)
Chiều cao mực nước bằng \(\dfrac{2}{3}\) chiều cao bể nên chiều cao mực nước là: \(3.\dfrac{2}{3}=2\left(m\right)\)
Lượng nước trong bể cũng có dạng một hình hộp chữ nhật với chiều dài \(2m\), chiều rộng \(1,5m\), chiều cao \(2m\).
Suy ra thể tích nước đã bơm vào bể là: \(2.1,5.2=6\left(m^3\right)\)
Đặc biệt:
Thể tích hình lập phương có cạnh \(a\) là:
\(V=a^3\)
Ví dụ 3: Một hình lập phương có cạnh \(2,5\left(cm\right)\). Tính thể tích hình lập phương đó?
Giải:
Thể tích hình lập phương là: \(2,5^3=15,625\left(cm^3\right)\)
Ví dụ 4: Một hình lập phương \(A\) có độ dài mỗi cạnh gấp đôi mỗi cạnh của hình lập phương \(B\). So sánh thể tích hai hình lập phương trên?
Giải:
Gọi độ dài mỗi cạnh hình lập phương \(A\) là \(a\)
Thì độ dài mỗi cạnh hình lập phương \(B\) là \(\dfrac{a}{2}\)
Do đó: Thể tích hình lập phương \(A\) là: \(V_A=a^3\)
Thể tích hình lập phương \(B\) là: \(V_B=\left(\dfrac{a}{2}\right)^3=\dfrac{a^3}{8}=\dfrac{V_A}{8}\)
Vậy \(V_B=\dfrac{V_A}{8}\) hay \(V_A=8.V_B\)
@1557461@