Bài 4: Hình lăng trụ đứng

1. Hình lăng trụ đứng

Cho hình vẽ:

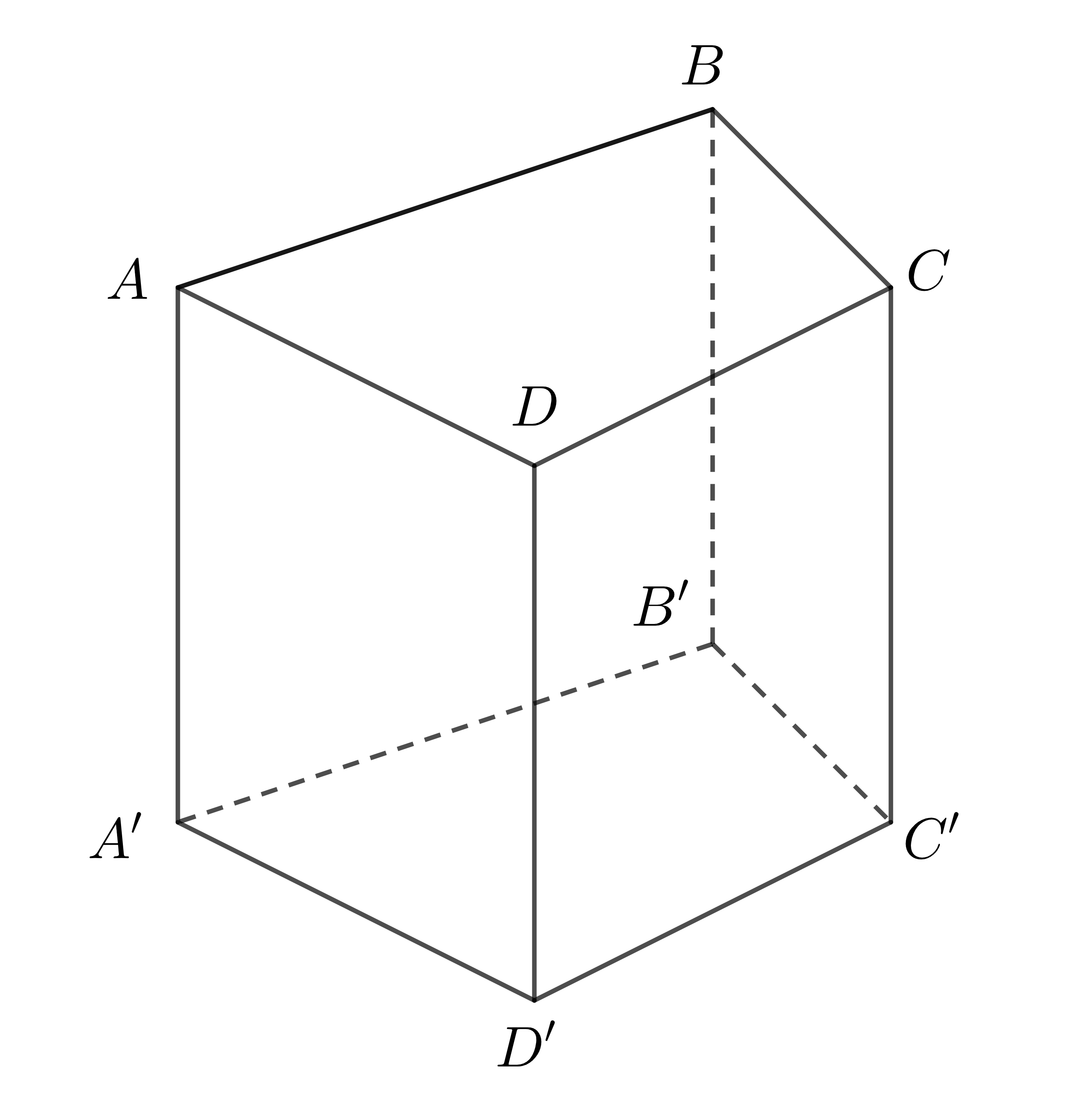
Hình vẽ trên là một ví dụ về hình lăng trụ đứng (hay lăng trụ đứng).

Trong hình vẽ trên:

      + \(A,B,C,D,A',B',C',D'\) là các đỉnh.

      + Các mặt \(ABB'A'\), \(ACC'A'\), \(BCC'B'\), \(ADD'A'\) là các mặt bên. Chúng đều là các hình chữ nhật.

      + Các đoạn \(AA',BB',CC',DD'\) là các cạnh bên. Chúng song song với nhau và bằng nhau và được gọi là chiều cao của lăng trụ đứng.

      + Hai mặt \(ABCD,A'B'C'D'\) là hai đáy, chúng là các hình tứ giác.

Do đó hình lăng trụ trên được gọi là hình lăng trụ đứng tứ giác và được kí hiệu là \(ABCD.A'B'C'D'\).

Nhận xét: Trong hình lăng trụ đứng:

       + Hai mặt đáy song song với nhau;

       + Các cạnh bên vuông góc với 2 mặt đáy;

       + Các mặt bên vuông góc với 2 mặt đáy.

Ví dụ: Xét trong hình lăng trụ tứ giác \(ABCD.A'B'C'D'\) :

     +  Hai đáy \(ABCD\) và \(A'B'C'D'\) nằm trong hai mặt phẳng song song. 

     + Các cạnh bên \(AA',BB',CC',DD'\) vuông góc với 2 đáy \(ABCD\) và \(A'B'C'D'\)

     + Các mặt bên \(\left(ABB'A'\right),\left(BCC'B'\right),\left(CDD'C'\right),\left(ADD'A'\right)\) vuông góc với 2 mặt đáy \(\left(ABCD\right)\) và \(\left(A'B'C'D'\right)\).

Chú ý: Hình hộp chữ nhật, hình lập phương cũng là các hình lăng trụ đứng;

           Hình lăng trụ đứng có đáy là hình bình hành được gọi là hình hộp đứng.

2. Ví dụ

Cho hình vẽ: 

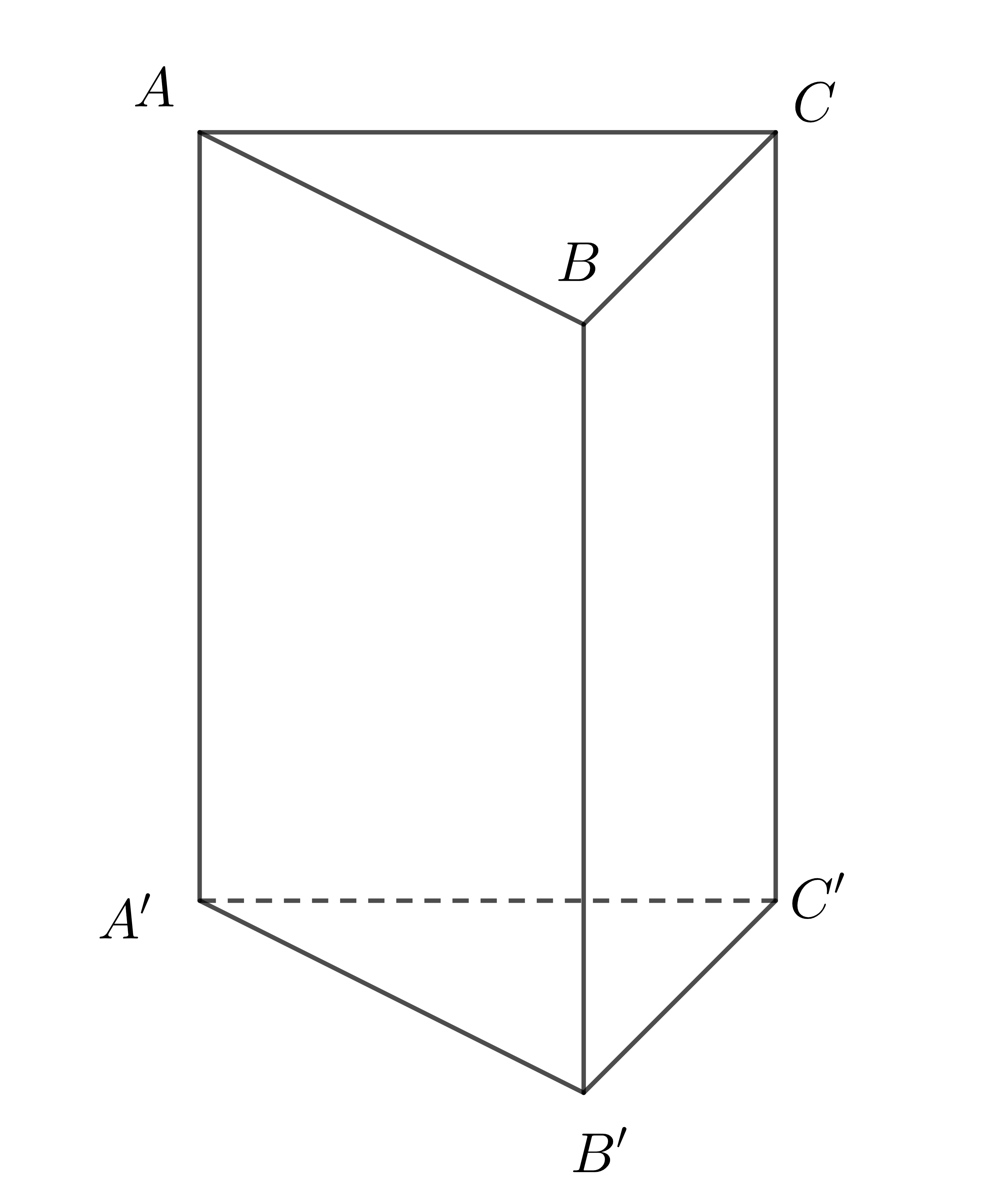
Hình vẽ trên được gọi là lăng trụ đứng tam giác và được kí hiệu là \(ABC.A'B'C'\)

Trong hình lăng trụ đứng \(ABC.A'B'C'\):

     + Các đỉnh là: \(A,B,C,A',B',C'\).

     + Các mặt bên là: \(ABB'A'\), \(BCC'B'\), \(ACC'A'\), chúng đều là các hình chữ nhật

     + Các cạnh bên là: \(AA',BB',CC'\) song song và bằng nhau, chúng được gọi là chiều cao của lăng trụ đứng.

     + Hai đáy là \(ABC\) và \(A'B'C'\) là các hình tam giác bằng nhau và nằm trong 2 mặt phẳng song song.

Tương tự như vậy, lăng trụ đứng ngũ giác có đáy là hình ngũ giác, lăng trụ đứng lục giác có đáy là hình lục giác,...

Ví dụ: \(GHIJK.G'H'I'J'K'\) là hình lăng trụ đứng ngũ giác:

- Chú ý: Khi vẽ hình lăng trụ đứng:

   + Các mặt bên là các hình chữ nhật, khi vẽ nó trên mặt phẳng, ta thường vẽ chúng là các hình bình hành;

   + Các cạnh song song vẽ thành các đoạn thẳng song song;

   + Các đoạn vuông góc có thể không vẽ thành các đoạn thẳng vuông góc.