Bài giải:
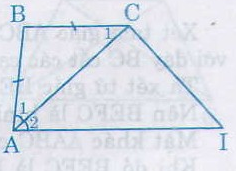
Ta có AB = BC (gt)
Suy ra ∆ABC cân
Nên (1)
Lại có (2) (vì AC là tia phân giác của )
Từ (1) và (2) suy ra
nên BC // AD (do ở vị trí so le trong)
Vậy ABCD là hình thang
Ta có AB = BC (gt)
Suy ra: ∆ABC cân.
Nên \(\widehat{A_1}=\widehat{C_1}\) (1)
Lại có \(\widehat{A_1}=\widehat{A_2}\) (2) (vì AC là tia phân giác của ˆAA^)
Từ (1) và (2) suy ra \(\widehat{C_1}=\widehat{A_2}\)
nên BC // AD (do \(\widehat{A_1};\widehat{C_2}\) ở vị trí so le trong)
Vậy ABCD là hình thang.

