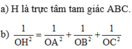Chúng ta biết rằng tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Vì vậy, ta có thể xem tứ diện OABC là một hình chữ nhật với cạnh OA, OB, OC.
Gọi SABC là diện tích của hình chữ nhật OABC. Ta có:
SABC = OA x OB
Gọi SHBC là diện tích của tam giác HBC. Ta có:
SHBC = 1/2 x HB x BC
Vì tứ diện OABC là một hình chữ nhật, nên ta có:
SOAB = OA x OB
Vậy, ta có:
(SOAB)2 = (OA x OB)2
= OA2 x OB2
= SABC x SHBC
= SABC + SHBC
Vậy, ta đã chứng minh được rằng (SOAB)2 = SABC + SHBC.