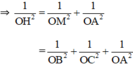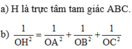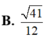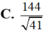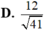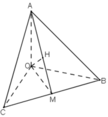
a) Ta có:
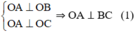
Do H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC) nên:
OH ⊥ (ABC) ⇒ OH ⊥ BC (2)
Mà OA; OH ⊂ (OAH); OA ∩ OH = O (3)
Từ (1); (2) và (3) ⇒ BC ⊥ (OAH)
⇒ BC ⊥ AH
Chứng minh tương tự ta có: AC ⊥ BH
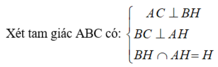
⇒ H là trực tâm ΔABC.
b) Gọi M = AH ∩ BC.
+ BC ⊥ (OAH) ⇒ BC ⊥ OM.
ΔOBC vuông tại O có đường cao OM
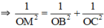
+ OA ⊥ (OBC) ⇒ OA ⊥ OM ⇒ ΔOAM vuông tại O.
OH ⊥ (ABC) ⇒ OH ⊥ AM.