Các câu hỏi tương tự
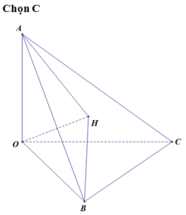
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau: I. H là trực tâm của
∆
ABC. II. H là trọng tâm của
∆
ABC. III.
1
O
H
2
1
O
A
2...
Đọc tiếp
Cho tứ diện OABC trong đó OA, OB, OC đôi một vuông góc. Gọi H là hình chiếu của O lên (ABC). Xét các mệnh đề sau:
I. H là trực tâm của ∆ ABC.
II. H là trọng tâm của ∆ ABC.
III. 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Số mệnh đề đúng là:
A. 0
B. 1
C. 2
D. 3
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Mệnh đề nào sau đây đúng A. H là trung điểm của AC B. H là trọng tâm tam giác ABC C. H là trung điểm của BC D. H là trực tâm của tam giác ABC
Đọc tiếp
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Mệnh đề nào sau đây đúng
A. H là trung điểm của AC
B. H là trọng tâm tam giác ABC
C. H là trung điểm của BC
D. H là trực tâm của tam giác ABC
Bài 6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mp(ABC)tại H. Chứng minh rằnga) OA⊥BC,OB⊥AC,OC⊥ABb) Gọi K là giao điểm của AH với BC. Chứng minh rằng AK⊥BCc) Gọi M là giao điểm của CH với AB. Chứng minh rằng AB⊥MC . Từ đó suy ra H là trực tâm tam giácABC.d)Bài 7. Cho hình chóp SABCD có đáy ABCD là hình chứ nhật có SA vuông góc với mp(ABCD). Chứng minhrằng các mặt bên của hình chóp là các tam giác vuông.Bài 8. Cho hình chóp SABCD có đáy ABCD là hình t...
Đọc tiếp
Bài 6. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Kẻ OH vuông góc với mp(ABC)
tại H. Chứng minh rằng
a) OA⊥BC,OB⊥AC,OC⊥AB
b) Gọi K là giao điểm của AH với BC. Chứng minh rằng AK⊥BC
c) Gọi M là giao điểm của CH với AB. Chứng minh rằng AB⊥MC . Từ đó suy ra H là trực tâm tam giác
ABC.
d)
Bài 7. Cho hình chóp SABCD có đáy ABCD là hình chứ nhật có SA vuông góc với mp(ABCD). Chứng minh
rằng các mặt bên của hình chóp là các tam giác vuông.
Bài 8. Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D với AD=DC=AB/2 . Gọi I là trung điểm của đoạn AB, SA vuông góc với mặt đáy. Chứng minh rằng
a) Tam giác ABC vuông tại C
b) CI⊥SB,DI⊥SC
c)CB⊥(SAC)
và các mặt bên hình chóp là các tam giác vuông
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA
a
2
2
, OB OC a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH A.
a
3
2
6
B.
a...
Đọc tiếp
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau, OA = a 2 2 , OB= OC =a. Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC) Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Chứng minh rằng (SOAB)2= SABC + SHBC
Cho hình chóp S. ABC có SA
⊥
(ABC) và ABC vuông tại C. Gọi O là tâm đường tròn ngoại tiếp tam giác SBC. H là hình chiếu vuông góc của O lên mặt phẳng (ABC). Khẳng định nào sau đây đúng? A. H là trọng tâm tam giác
△
ABC B. H là tâm đường tròn nội tiếp tam giác
△
ABC C. H là trung điểm cạnh AC D. H là trung điểm cạnh AB
Đọc tiếp
Cho hình chóp S. ABC có SA ⊥ (ABC) và ABC vuông tại C. Gọi O là tâm đường tròn ngoại tiếp tam giác SBC. H là hình chiếu vuông góc của O lên mặt phẳng (ABC). Khẳng định nào sau đây đúng?
A. H là trọng tâm tam giác △ ABC
B. H là tâm đường tròn nội tiếp tam giác △ ABC
C. H là trung điểm cạnh AC
D. H là trung điểm cạnh AB
Cho hình chóp S.ABC có đáy ABC là tam giác đều, I là trung điểm của BC, SA vuông góc với (ABC). Gọi H, O lần lượt là trực tâm của tam giác SBC, ABC, K là giao điểm của hai đường thẳng SA và OH. Chứng minh rằng:
a) OH vuông góc với (SBC)
b) SO vuông góc với IK.
Cho tứ diện S.ABC có SA và SB vuông góc với nhau, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trực tâm H của tam giác ABC. Chứng minh: 6(SA2 + SB2 + SC2) ≥ (AB + BC + CA)2.
Cho tứ diện ABCD có tam giác ABC là tam giác đều cạnh a, AD vuông góc với BC, AD = a và khoảng cách từ điểm D đến đường thẳng BC là a . Gọi H là trung điểm BC, I là trung điểm AH. Chứng minh rằng đường thẳng DI vuông góc với mặt phẳng (ABC).