Question

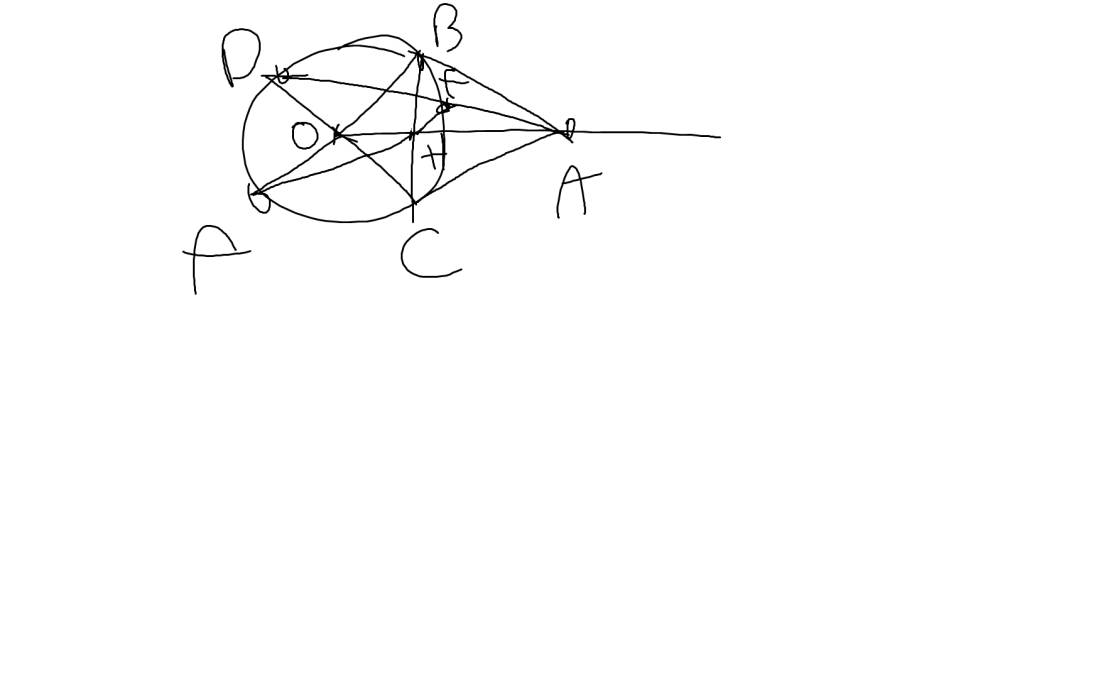
Từ điểm A nằm bên ngoài đường tròn (O) vẽ 2 tiếp tuyến AB và AC của (O) lần lượt tại B và C. 

a. C/m tứ giác ABOC nội tiếp đường tròn.

b. Vẽ đường kính CD của (O), gọi E là giao điểm của AD và  (O), biết E và D. C/m AD.AE = AB²

c. Gọi H là giao điểm của AO và BC, vẽ đường kính BF của  (O). C/m 3 điểm E,H,F thẳng hàng.

vẽ hình nữa nha

Answer 1

a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

b: Xét (O) có

ΔCED nội tiếp

CD là đường kính

Do đó: ΔCED vuông tại E

=>CE\(\perp\)AD tại E

Xét (O) có

AB,AC là các tiếp tuyến

Do đó: BA=AC

Xét ΔCDA vuông tại C có CE là đường cao

nên \(AE\cdot AD=AC^2\)

=>\(AE\cdot AD=AB^2\)